행렬(Metric) 이란?
행렬(Metric)
X=⎣⎢⎡17−2−25−1302⎦⎥⎤
소문자 볼드체(x)는 벡터, 대문자 볼드체(X)는 행렬을 의미한다.
: 벡터를 원소로 갖는 2차원 배열(array)을 의미한다.
[코드]
X = np.array([[ 1, -2, 3],
[ 7, 5, 0],
[-2, -1, 2]])
numpy는 행(row)을 기본 단위로 처리한다.
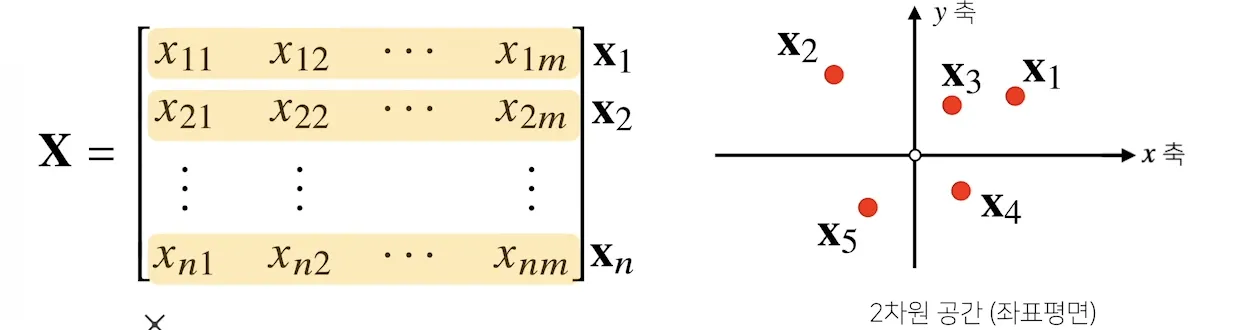
X=⎣⎢⎢⎢⎢⎡x1x2⋮xn⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡x11x21⋮xn1x12x22⋮xn2⋯⋯⋱⋯x1mx2m⋮xnm⎦⎥⎥⎥⎥⎤
-
크기가 n×m 이면, 원소는 xij로 표기한다. (i : 행, j : 열)
-
공간상에서의 벡터는 한 점을 나타낸다면, 행렬은 여러 점을 나타낸다.
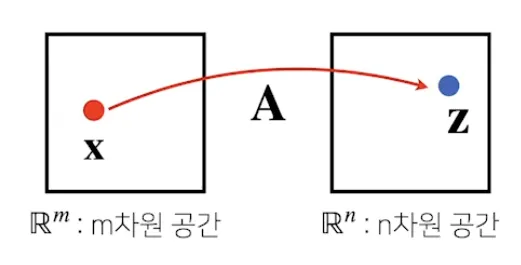
- 행렬은 벡터 공간에서 사용되는 연산자 (operator)로도 작동한다.
zi=∑j=1maijxj,z=⎣⎢⎢⎢⎢⎡z1z2⋮zn⎦⎥⎥⎥⎥⎤=A⎣⎢⎢⎢⎢⎡a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1ma2m⋮anm⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡x1x2⋮xm⎦⎥⎥⎥⎥⎤
⇒ 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다. (패턴 추출, 데이터 압축 등 가능)
행렬의 기본 연산
행렬 X, Y가 다음과 같다고 하자
X=⎣⎢⎢⎢⎢⎡x11x21⋮xn1x12x22⋮xn2⋯⋯⋱⋯x1mx2m⋮xnm⎦⎥⎥⎥⎥⎤Y=⎣⎢⎢⎢⎢⎡y11y21⋮yn1y12y22⋮yn2⋯⋯⋱⋯y1my2m⋮ynm⎦⎥⎥⎥⎥⎤
: 이때 행렬끼리 동일한 모양이라면 연산이 가능하다.
-
스칼라곱 (Scalar Multiplication) : αX=(αxij)
: 모든 성분에 똑같이 숫자를 곱하는 것을 의미한다.
αX=⎣⎢⎢⎢⎢⎡αx11αx21⋮αxn1αx12αx22⋮αxn2⋯⋯⋱⋯αx1mαx2m⋮αxnm⎦⎥⎥⎥⎥⎤
-
덧셈·뺄셈 (Addition·Subtraction) : X±Y=(xij±yij)
X±Y=⎣⎢⎢⎢⎢⎡x11±y11x21±y21⋮xn1±yn1x12±y12x22±y22⋮xn2±yn2⋯⋯⋱⋯x1m±y1mx2m±y2m⋮xnm±ynm⎦⎥⎥⎥⎥⎤
-
성분곱 (Hadamard Product) : X⊙Y=(xijyij)
Hadamard 곱, 또는 성분곱은 동일한 위치의 성분을 각각 곱하는 것을 의미한다.
X⊙Y=⎣⎢⎢⎢⎢⎡x11y11x21y21⋮xn1yn1x12y12x22y22⋮xn2yn2⋯⋯⋱⋯x1my1mx2my2m⋮xnmynm⎦⎥⎥⎥⎥⎤
※ 행렬의 스칼라곱, 덧셈, 뺄셈, 성분곱은 벡터와 다를 게 없다.
-
행렬곱 (Matrix Multiplication) : i번째 행벡터와 j번째 열벡터 사이의 내적
행렬곱의 특징
-
X의 열 수와 Y의 행 수가 같아야 한다.
-
행렬곱은 교환법칙이 성립하지 않기 때문에, 곱하는 순서가 바뀌면 결과도 달라진다. (XY=YX)
-
모든 선형변환(linear transform)은 결국 행렬곱 형태로 표현 가능하다.
행렬곱의 일반적인 수식은 아래와 같다:
XY=(∑kxikykj)
[코드]
X = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
Y = np.array([[0, 1],
[1, -1],
[-2, 1]])
X @ Y
⚠️np.inner 함수와의 차이⚠️
한편 np.inner(X, Y)는 행렬곱과는 다르게 작동한다.
이는 i번째 행벡터와 j번째 행벡터 사이의 내적(inner product)을 계산하며,
결과적으로 tr(XY⊤)와 같은 동작을 수행하게 된다.
즉, X의 행의 개수와 Y의 행의 개수가 같아야 연산이 가능하다.
이 때문에 행렬곱과는 차원 조건도 다르고 결과도 완전히 다르다.
아래는 np.inner의 예시이다:
X = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
Y = np.array([[0, 1, -1],
[1, -1, 0]])
np.inner(X, Y)
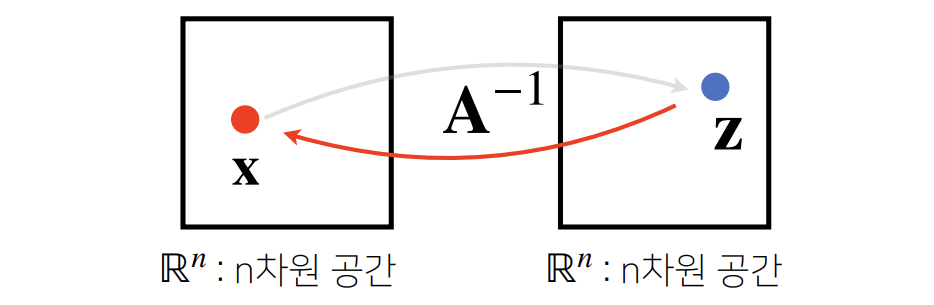
역행렬 (Inverse Matrix)
: 어떤 행렬 A에 대해, 그 연산을 거꾸로 되돌리는 역할을 하는 행렬을 의미하며,
보통 A−1로 표기한다.
역행렬은 행과 열의 개수가 같고(즉, 정방행렬) 행렬식(determinant)이 0이 아닌 경우에만 계산할 수 있다.
AA−1=A−1A=I,I=⎣⎢⎢⎢⎢⎡10⋮001⋮0⋯⋯⋱⋯00⋮1⎦⎥⎥⎥⎥⎤
NumPy에서는 np.linalg.inv()를 사용하여 역행렬을 구할 수 있다.
X = np.array([[1, -2, 3],
[7, 5, 0],
[-2, -1, 2]])
np.linalg.inv(X)
X @ np.linalg.inv(X)
⚠️ 역행렬을 구할 수 없는 경우 ⚠️
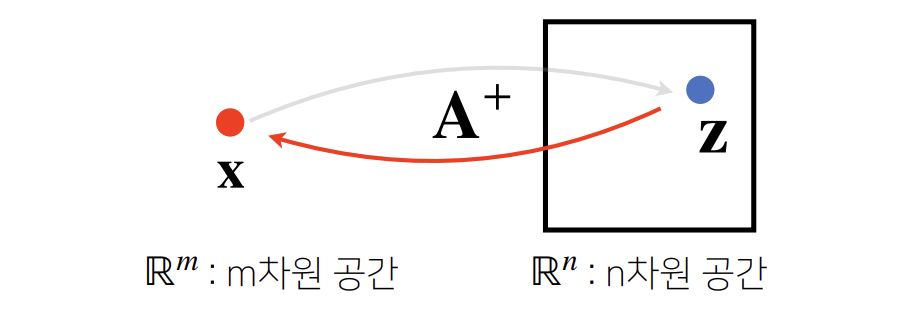
: 만약 행렬의 행과 열 수가 다르거나, 행렬식이 0인 경우에는 역행렬이 존재하지 않는다.
이러한 경우에는 유사역행렬(pseudo-inverse) 또는 무어-펜로즈 역행렬(Moore-Penrose pseudoinverse)을 사용한다.
무어-펜로즈 유사역행렬 (Moore-Penrose Pseudoinverse)
: 행렬 A가 n×m 행렬이고, 전치행렬 AA⊤ 은 m×n일 때,
다음 두 가지 경우로 나뉜다.
-
n≥m 인 경우 :
A+=(A⊤A)−1A⊤
이 경우에는 A+A=I가 성립한다.
A⊤A는 m×m 행렬이므로 역행렬 계산이 가능하다.
-
n≤m 인 경우 :
A+=A⊤(AA⊤)−1
이 경우에는 AA+=I가 성립한다.
A⊤A는 m×m 행렬이므로 역행렬 계산이 가능하다.
따라서, 유사역행렬을 구할 때는 행의 개수와 열의 개수를 비교하여 적절한 공식을 선택해야 한다.
NumPy에서는 np.linalg.pinv()를 사용하여 유사역행렬을 쉽게 구할 수 있다.
Y = np.array([[0, 1],
[1, -1],
[-2, 1]])
np.linalg.pinv(Y)
np.linalg.pinv(Y) @ Y
✅ 예제 1: 연립방정식 풀기
변수의 개수가 식의 개수보다 많을 때 (n≤m)의 예제를 생각해보자.
이 경우는 해가 유일하지 않거나 무한히 존재할 수 있는 상황으로, 다음과 같이 정리된다.
a11x1+a12x2+⋯+a1mxma21x1+a22x2+⋯+a2mxm⋮an1x1+an2x2+⋯+anmxm=b1=b2⋮=bn→Ax=b
여기서 a는 계수, x1, x2,⋯,xm는 구하고자 하는 해를 의미한다.
이 식은 행렬 방정식 형태로 표현할 수 있으며,
해를 구하기 위해 유사역행렬(Moore-Penrose Pseudo-Inverse)을 이용한다.
x=A+b=A⊤(AA⊤)−1b
이처럼 유사역행렬을 이용하면 과잉 결정된 시스템에서도 최적의 해(근사해)를 구할 수 있다.
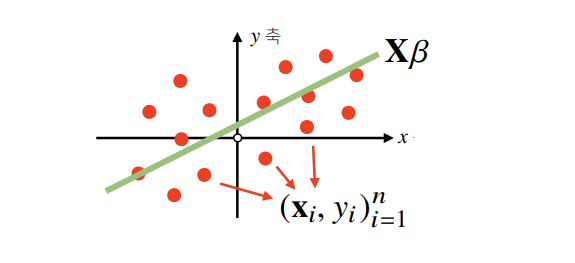
✅ 예제 2: 선형회귀(Linear Regression) 분석
이번에는 반대 상황, 즉 식의 개수 n가 변수의 개수 m보다 많은 경우(n≤m) 를 살펴보자.
이는 다음과 같은 선형 모델 식으로 표현할 수 있다.
⎣⎢⎢⎢⎢⎡x1x2⋮xn⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡β1β2⋮βm⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡y1y2⋮yn⎦⎥⎥⎥⎥⎤ Xβ =y
여기서 X는 설명 변수(feature), y는 타깃 값(target), β는 추정해야 할 계수이다.
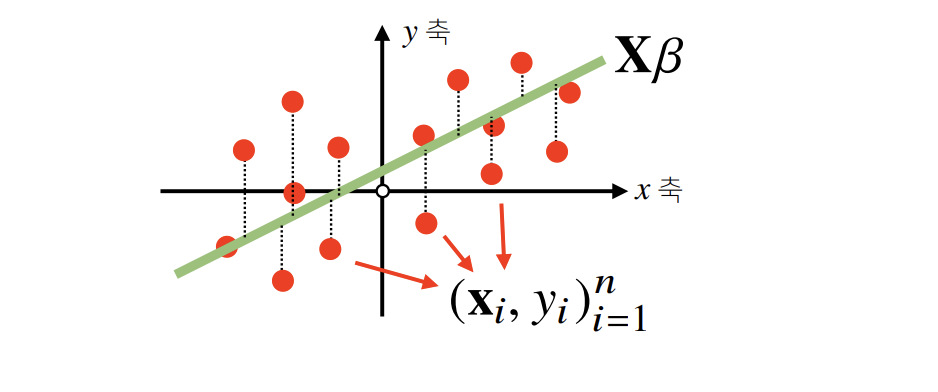
그러나 일반적으로 Xβ=y를 정확히 만족하는 해는 존재하지 않으며,
가장 적합한 해를 구하기 위해 다음과 같은 근사식을 사용한다.
Xβ=y^≈y
이때, 다음 목적식을 최소화한다.
min∣∣y−y^∣∣2
즉, L2 노름을 최소화하는 계수 β를 찾는 것이 목표이다.
이때 유사역행렬을 이용한 해는 다음과 같이 계산된다.
β=X+y=(X⊤X)−1X⊤y
[코드]
다음은 동일한 선형회귀 문제를 두 가지 방식으로 해결하는 코드 예제이다:
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X, y)
y_test = model.predict(x_test)
X_ = np.array([np.append(x, [1]) for x in X])
beta = np.linalg.pinv(X_) @ y
y_test = np.append(x_test) @ beta
np.linalg.pinv()를 활용하면 LinearRegression()과 동일한 결과를 수학적으로 직접 구현할 수 있다.
이처럼 선형 방정식과 회귀 문제 모두 유사역행렬로 해결이 가능하다는 점은 수치해석과 머신러닝의 핵심 개념 중 하나이다.
위 내용은 (([부스트캠프 AI Tech 프리코스] 인공지능 기초 다지기 (2)) 2. 행렬이 뭐에요?) 강의 내용을 바탕으로 작성하였습니다.
더 자세한 내용은 강의를 통해 확인하시길 바랍니다.