[BoostCamp Pre-course] 경사하강법(Gradient Descent) 개념 정리

1. 미분(differentiation)이란?

미분은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로,
최적화에서 가장 많이 사용되는 기법이다.

미분은 다음과 같은 극한의 형태로 정의된다.

즉, 변화율의 극한($limit$)으로 정의되며,
함수 $f$의 주어진 점 $(x,f(x))$에서의 접선의 기울기를 의미한다.

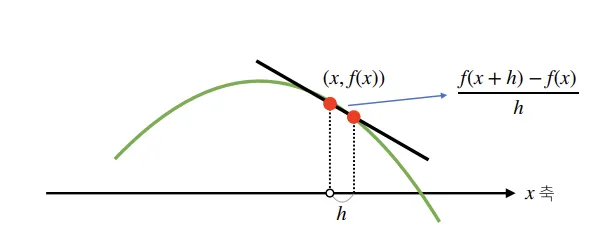
이때 $h$를 0으로 보내는 과정( $\lim_{h \to 0}$ )에서
함수가 매끄럽게 연속되어 있어야 미분이 가능하다.

미분값의 해석

미분값을 통해 함수값이 증가하거나 감소하는 방향을 판단할 수 있다.

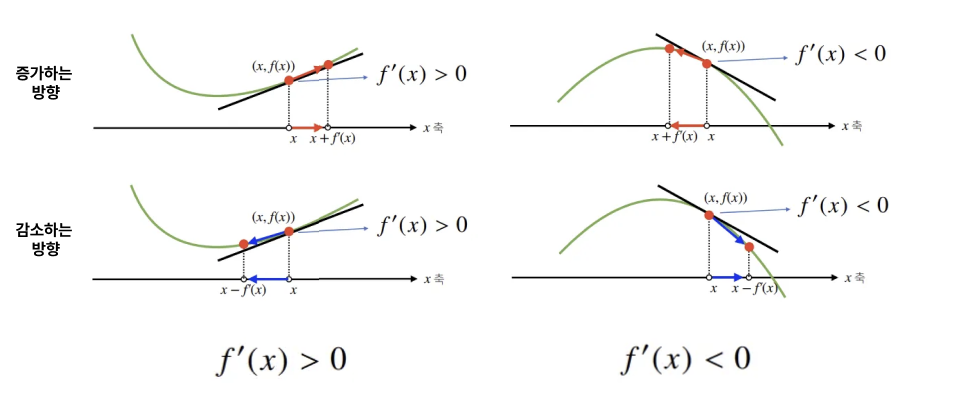
• 미분값이 양수일 경우( $f'(x) > 0$ ) : 함수가 증가함

• 미분값이 음수일 경우( $f'(x) < 0$ ) : 함수가 감소함

이를 통해 두 가지 최적화 알고리즘을 정의할 수 있다.

• 경사상승법 (Gradient Ascent)
  미분값을 더해서 함수의 극대값을 찾는다.
  목적함수가 최대값에 도달하면 업데이트를 멈춘다.

• 경사하강법 (Gradient Descent)
  미분값을 빼서 함수의 극소값을 찾는다.
  목적함수가 최소값에 도달하면 업데이트를 멈춘다.

[예제]
다음과 같은 함수 $f(x)$에 대해 미분을 수행해보자.

위 결과는 정의에 따라 다음과 같은 극한식을 전개한 뒤 계산할 수 있다.

따라서 $h→0$일 때, $f'(x)=2x+2$가 된다.

[코드]

import sympy as sym
from sympy.abc import x

sym.diff(sym.poly(x**2 + 2*x + 3), x)
# 결과: Poly(2x + 2, x, domain=Z)

sympy 라이브러리를 통해 미분 계산을 자동으로 수행할 수 있다.

---

2. 편미분 (Partial Differentiation)

변수가 여러 개인 함수의 경우, 한 변수에 대해서만 미분하는 편미분을 사용한다.

여기서 $e_i$ 는 단위벡터로, $i$번째 변수에만 영향을 준다.
이를 통해 특정 방향의 변화율을 계산할 수 있다.

[예제]
예를 들어, 다음과 같은 함수가 있다고 하자.

이 함수에 대해 $x$ 방향의 편미분(즉, $x$에 대한 변화율)을 계산하면 다음과 같다:

여기서 중요한 점은, 편미분을 계산할 때는 다른 변수는 모두 상수로 간주한다는 것이다.즉, 위 식에서 $y$는 상수로 보고 $x$에 대해서만 미분을 수행한 결과다.

따라서 $x$ 방향으로만 함수가 어떻게 변화하는지를 알고 싶을 때는 이와 같이 $\frac{\partial f}{\partial x}$를 통해 계산하면 된다.

[코드]

import sympy as sym
from sympy.abc import x, y

sym.diff(sym.poly(x**2 + 2*x*y + 3) + sym.cos(x + 2*y), x)
# 결과: 2x + 2y − sin(x + 2y)

---

3. 그레디언트(Gradient) 벡터

벡터 $\mathbf x = (x_1, \cdots, x_d)$ 로 구성된 $d$-차원 입력에 대해, 함수 $f(x)$의 변화율을 각 방향마다 계산한 결과를 그레디언트 벡터(gradient vector)라고 한다.

즉, 다변수 함수에서 모든 변수에 대한 편미분 결과를 모은 벡터값이라고 생각하면 된다.

이를 수식으로 표현하면 다음과 같다:

그레디언트 벡터는 해당 지점에서 함수값이 가장 빠르게 증가하는 방향을 의미하며, 반대로 가장 빠르게 감소하는 방향은 그레디언트 벡터의 부호를 반대로 취한 $-\nabla f$가 된다. 이 개념은 경사하강법(gradient descent)에서 매우 핵심적인 역할을 한다.

이제 위 개념을 시각적으로 이해해보자.

$f(x, y) = x^2 + 2y^2$라고 할 때,

각 점 $(x, y, z)$ 공간에서 $f(x, y)$ 표면을 따라 $\nabla f$, $-\nabla f$벡터를 그리면
아래와 같이 그려진다.

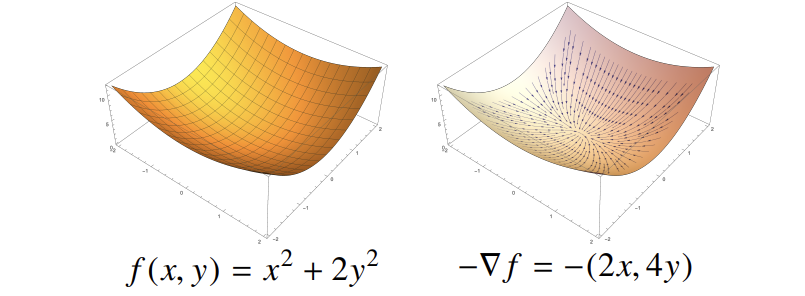
함수의 등고선(contour) 그래프로 보면,
중심부로 갈수록 함수값이 낮아지는 구조를 확인할 수 있다.

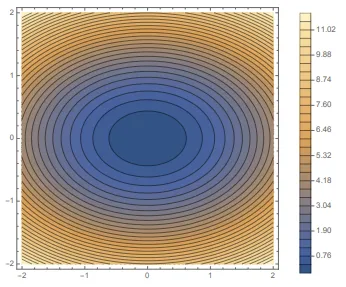
파란색 중심은 최소값을 의미하고, 바깥으로 갈수록 함수값이 커지는 것을 알 수 있다.

• $\nabla f = (2x, 4y)$ :
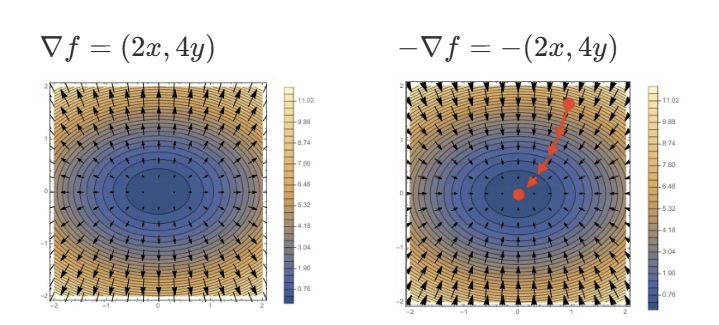
  각 점에서의 그레디언트 벡터를 화살표로 표현하면 왼쪽과 같다.
  모든 벡터는 함수의 증가 방향(즉, 기울기가 증가하는 방향)을 가리키고 있다.

• $-\nabla f = -(2x, 4y)$ :
  각 점에서의 그레디언트 벡터의 반대 방향을 화살표로 표현하면 오른쪽과 같다.
  이 벡터는 함수의 가장 빠른 감소 방향을 나타내며,
  경사하강법(gradient descent)이 따라가는 방향이다.

---

4. 경사하강법 (Gradient Descent)

경사하강법은 함수의 최소값을 찾기 위해 반복적으로 미분값을 빼는 방식으로 최적점을 탐색하는 알고리즘이다.

단변수 함수일 경우

입력:

• gradient: 미분을 계산하는 함수
• init: 시작점
• lr: 학습률 (learning rate) — 업데이트 속도를 조절
• eps: 종료조건 — 컴퓨터로는 정확히 0에 도달할 수 없기 때문에 필요

출력: var

[코드]

# 경사하강법 알고리즘
var = init
grad = gradient(var)
while(abs(grad) > eps):
    var = var - lr * grad
    grad = gradient(var)

[예제 코드]

def func(val):
    fun = sym.poly(x**2 + 2*x + 3)
    return fun.subs(x, val), fun

def func_gradient(fun, val):
    _, function = fun(val)
    diff = sym.diff(function, x)
    return diff.subs(x, val), diff

def gradient_descent(fun, init_point, lr_rate=1e-2, epsilon=1e-5):
    cnt = 0
    val = init_point
    diff, _ = func_gradient(fun, init_point)
    while abs(diff) > epsilon:
        val = val - lr_rate * diff
        diff, _ = func_gradient(fun, val)
        cnt += 1

    print("함수: {}, 연산횟수: {}, 최소점: ({}, {})".format(fun(val)[1], cnt, val, fun(val)[0]))

gradient_descent(fun=func, init_point=np.random.uniform(-2, 2))

다변수 함수일 경우

벡터 형태의 그레디언트를 사용하기 때문에, 반복문 조건에서 abs() 대신 np.linalg.norm()을 사용한다.

[코드]

# 경사하강법 알고리즘
var = init
grad = gradient(var)
while(norm(grad) > eps):
    var = var - lr * grad
    grad = gradient(var)

[예제 코드]

def eval_(fun, val):
    val_x, val_y = val
    return fun.subs(x, val_x).subs(y, val_y)

def func_multi(val):
    x_, y_ = val
    func = sym.poly(x**2 + 2*y**2)
    return eval_(func, [x_, y_]), func

def func_gradient(fun, val):
    x_, y_ = val
    _, function = fun(val)
    diff_x = sym.diff(function, x)
    diff_y = sym.diff(function, y)
    grad_vec = np.array([eval_(diff_x, [x_, y_]), eval_(diff_y, [x_, y_])], dtype=float)
    return grad_vec, [diff_x, diff_y]

def gradient_descent(fun, init_point, lr_rate=1e-2, epsilon=1e-5):
    cnt = 0
    val = init_point
    diff, _ = func_gradient(fun, val)
    while np.linalg.norm(diff) > epsilon:
        val = val - lr_rate * diff
        diff, _ = func_gradient(fun, val)
        cnt += 1

    print("함수: {}, 연산횟수: {}, 최소점: ({}, {})".format(fun(val)[1], cnt, val, fun(val)[0]))

pt = [np.random.uniform(-2, 2), np.random.uniform(-2, 2)]
gradient_descent(fun=func_multi, init_point=pt)
# 함수: Poly(x**2 + 2*y**2, x, y, domain='ZZ'), 연산횟수: 630, 최소점: ([-4.96e-06, -5.05e-12], 2.46e-11)

이처럼 미분과 경사하강법은 함수 최적화와 딥러닝에서 필수적인 개념이며,
단변수/다변수 함수에 따라 그 적용 방식과 계산 과정에 차이가 있다.
파이썬의 sympy와 numpy 라이브러리를 활용하면 이러한 수학적 개념을 직접 구현하고 실험해볼 수 있다.

---

위 내용은 (([부스트캠프 AI Tech 프리코스] 인공지능 기초 다지기 (2)) 3. 경사하강법) 강의 내용을 바탕으로 작성하였습니다.
더 자세한 내용은 강의를 통해 확인하시길 바랍니다.