[BoostCamp Pre-course] 벡터(Vector) 개념 정리

벡터(Vector)란?

벡터(Vector)

$\mathbf{x} = \begin{bmatrix} 1 \\ 7 \\ 2 \end{bmatrix} \qquad\mathbf{x}^\top = [1, 7, 2]$

왼쪽은 열벡터, 오른쪽은 행벡터를 뜻한다.
: 숫자를 원소로 가지는 리스트 (list) / 배열(array)을 의미한다.

[코드]

x = [1, 7, 2]
x = np.array([1, 7, 2])

• np.array로 생성하면 기본적으로 행벡터로 처리한다.

• 벡터는 공간에서의 한 점, 즉 원점으로부터의 상대적 위치를 나타낸다.
  

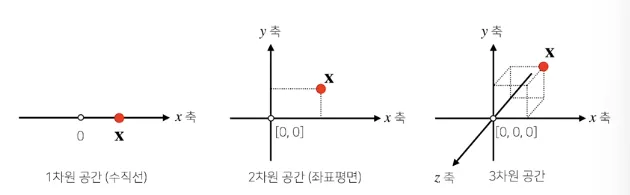
• 차원(Dimension) : 배열 안 원소(숫자)의 개수

  • 𝑑개의 숫자를 담으면 𝑑차원 벡터라고 부른다.

  • 인공지능·머신러닝 분야에서는 수백 ~ 수천 차원의 벡터가 흔히 쓰인다

---

벡터의 기본 연산

: 덧셈, 뺄셈, Hadamard 곱은 모두 두 벡터의 차원이 같을 때만 연산이 가능하다.

1. 스칼라곱 (Scalar Multiplication)

   : 벡터에 실수 𝛼를 곱하면

   $\alpha\,\mathbf{x} = \alpha\begin{bmatrix}x_1\\x_2\\\vdots\\x_d\end{bmatrix}=\begin{bmatrix}\alpha x_1\\\alpha x_2\\\vdots\\\alpha x_d\end{bmatrix}$

   길이가 $|α|$배로 늘거나 줄어든다. 이때 $α<0$이면 방향이 반대가 된다.

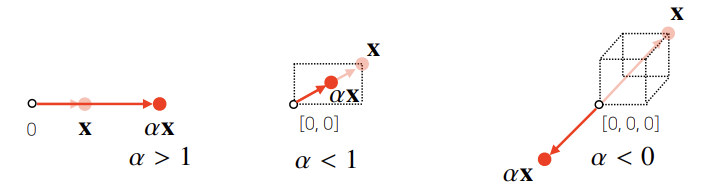
2. 벡터 덧셈 (Vector Addition)

   벡터끼리의 덧셈은 각 성분을 같은 위치끼리 더하는 것을 의미한다.

   두 벡터 $a$와 $b$가 다음과 같을 때:
   
   

   $\mathbf{a} = \begin{bmatrix}a_1 \\a_2 \\\vdots \\a_d\end{bmatrix}, \quad\mathbf{b} = \begin{bmatrix}b_1 \\b_2 \\\vdots \\b_d\end{bmatrix} , \quad \mathbf{a} + \mathbf{b} = \begin{bmatrix}a_1 + b_1 \\a_2 + b_2 \\\vdots \\a_d + b_d\end{bmatrix}$

   이때 덧셈 결과는 다음과 같이 각 성분끼리 더해진다
   
   

3. 벡터 뺄셈 (Vector Subtraction)

   벡터의 뺄셈도 성분별로 이루어지며 다음과 같이 표현된다:

   $\mathbf{a} - \mathbf{b} = \begin{bmatrix}a_1 - b_1 \\a_2 - b_2 \\\vdots \\a_d - b_d\end{bmatrix}$

   벡터 $a$에서 $b$를 뺀 결과는 두 벡터 사이의 방향과 거리를 나타낸다.

4. 성분곱 (Hadamard Product)

   Hadamard 곱, 또는 성분곱은 동일한 위치의 성분을 각각 곱하여 벡터로 반환한다:

   $\mathbf{a} \odot \mathbf{b} = \begin{bmatrix}a_1 \cdot b_1 \\a_2 \cdot b_2 \\\vdots \\a_d \cdot b_d\end{bmatrix}$

   또는 NumPy에서처럼 다음처럼 쓰일 수 있다:

   $\mathbf{a} * \mathbf{b} = \begin{bmatrix}a_1 \cdot b_1 \\a_2 \cdot b_2 \\\vdots \\a_d \cdot b_d\end{bmatrix}$

---

노름(norm)

: 벡터가 원점에서 얼마나 떨어져 있는지를 재는 거리 함수다.

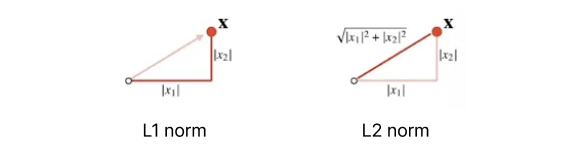
• 노름 종류를 바꾸면 등거리 곡선의 모양이 달라진다.

• 문제 특성이나 규제 목적에 따라 적절히 선택한다.

L1-노름

: 각 성분의 변화량의 절대값

$||x||_1 = \Sigma_{i=1}^d |x_i|$

def l1_norm(x):
    x_norm = np.abs(x)
    x_norm = np.sum(x_norm)
    return x_norm

L2-노름

: 피타고라스 정리 이용 , 유클리드 거리

$||x||_2 = \sqrt{\Sigma_{i=1}^d |x_i|^2}$

# ver 1
 def l2_norm(x):
     x_norm = x*x
     x_norm = np.sum(x_norm)
     x_norm = np.sqrt(x_norm)
     return x_norm
 # ver 2
 def l2_norm(x):
 	return np.linalg.norm(x)

L2 노름을 활용한 각도 계산

: 두 벡터 $x$, $y$의 각도 $\theta$를 구하려면 L2-노름을 이용해 코사인 법칙을 적용한다.

위의 분자를 전개하면

따라서 최종적으로

각도를 구하는 코드는 다음과 같다.

def angle(x, y):
	v = np.inner(x, y) / (l2_norm(x) * l2_norm(y))
	theta = np.arccos(v)
	return theta 

cf) 내적(Inner Product)과 정사영(Projection)의 의미

벡터 $x$와 $y$ 사이의 내적(inner product)은 다음과 같은 기하학적 의미를 가진다:

$<x, y> = ||x||_2||y||_2cos\theta$

이 식은 벡터 간 유사도(similarity)를 나타내는 대표적인 수식으로,
벡터 $x$ 벡터 $y$ 방향으로 얼마나 같은 방향을 향하고 있는지를 수치로 보여준다.

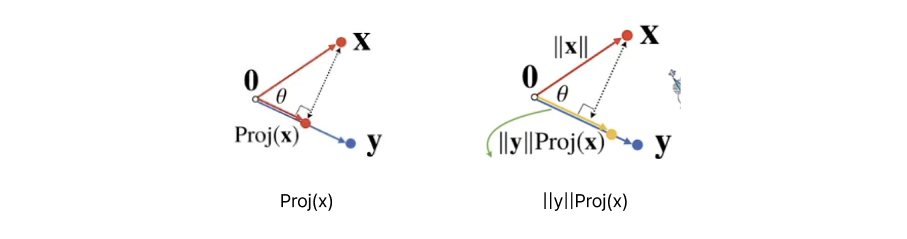
[왼쪽]

벡터 $x$를 $y$ 방향으로 정사영(Projection) 했을 때의 그림자는 다음과 같다:

$Proj(x) = ||x|| cos \theta$ (코사인 법칙)

이 값은 벡터$x$가 $y$ 방향으로 얼마나 드리워졌는지(그림자 길이)를 뜻한다.

[오른쪽]

이제 이 정사영된 길이를 벡터 $y$의 크기만큼 다시 조정하면,
즉 $||y||_2$를 곱하면 내적이 된다:

$<x, y> = |y||_2 ⋅ Proj(x)$

즉, 내적은 "벡터 $x$의 그림자(정사영)를 $y$의 크기에 맞춰 조정한 값"으로 해석할 수 있다.

결국 내적은 두 벡터의 방향 유사도를 나타내고,

동시에 벡터 $x$가 $y$ 방향으로 얼마나 포함되는지를 수치로 표현한다.

따라서 내적은 기하학적으로는 정사영의 길이 × 대상 벡터의 크기,
수학적으로는 벡터 간 유사도 척도로 이해할 수 있다.

---

위 내용은 (([부스트캠프 AI Tech 프리코스] 인공지능 기초 다지기 (2)) 1. 벡터가 뭐에요?) 강의 내용을 바탕으로 작성하였습니다.
더 자세한 내용은 강의를 통해 확인하시길 바랍니다.