문제 설명
이 문제는 아주 평범한 배낭에 관한 문제이다.
한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다닐 배낭 또한 최대한 가치 있게 싸려고 한다.
준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다. 아직 행군을 해본 적이 없는 준서는 최대 K만큼의 무게만을 넣을 수 있는 배낭만 들고 다닐 수 있다. 준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값을 알려주자.
입력
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)가 주어진다.
입력으로 주어지는 모든 수는 정수이다.
출력
한 줄에 배낭에 넣을 수 있는 물건들의 가치합의 최댓값을 출력한다.
예제
문제 분석
이제 곧 546박 547일짜리 여행을 떠날텐데 그 전에 또 여행을 가려고 하는 준서. 준서가 여행 가방을 싸려고 하는데, 각각의 물건들은 무게(W)와 가치(V)를 가진다. 이 때 가방에 담은 물건들의 가치의 합이 최대가 되도록 물건을 담았을 때, 그 최댓값을 구하는 문제이다.
접근 방법
완전탐색
처음에 문제를 읽으면 완전탐색을 떠올리기 쉽다. 각 물품마다 넣거나 넣지 않는 두 가지의 선택지가 존재하고, 모든 경우를 다 살펴봐야지 가치합의 최댓값을 알 수 있지 않을까? 하는 생각에 완전탐색을 시도하게 된다.
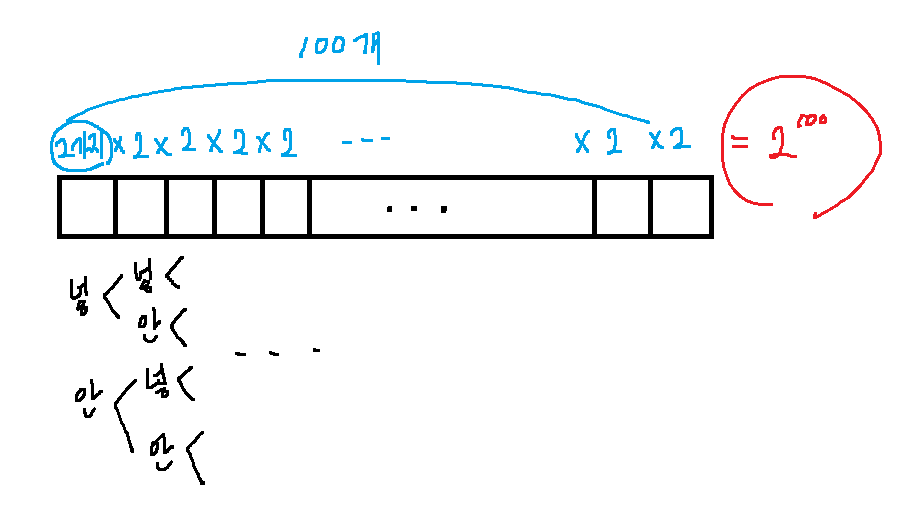
항상 완전탐색을 시도하기 전엔 시간복잡도를 간단하게라도 계산해보자. N의 최댓값이 100이라 얼핏 가능할 것 같기도 하지만, 이 100개의 물건마다 넣거나 넣지 않는 두 가지의 선택지가 있고, 이 사건들은 동시에 일어나기 때문에 곱 연산을 해줘야 한다. 그렇게 되면 총 연산횟수가 대략 2의 100제곱이 된다.
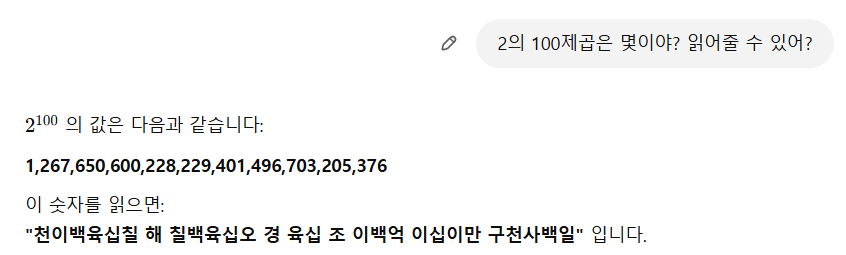
뭐 대략 이런 숫자라고 한다. 컴퓨터가 1초에 1억번 정도 연산한다고 했을 때 이 연산을 끝내기 위해서는 403경 년이 걸린다고 한다. 이런 이유에서 완전탐색은 넣어두도록 하자.
다이나믹 프로그래밍(DP)
완전탐색이나 백트래킹으로 문제를 풀다가 시간복잡도에서 문제가 생길 경우 DP로 해결가능한지 반드시 검토해 보자! 사실 나도 배낭 문제를 처음 풀었을 당시에는 혼자서 풀이법을 떠올리지 못 했다. DP라 함은 이전 상태에 기반해서 현재 상태를 유추하는 방식으로 최적해를 찾아 나가는 풀이법인데, 어떤 상태를 변수로 두고 DP를 구현해야할 지 전혀 감이 오지 않았기 때문이다.
기존에 풀었던 DP 문제들은 한 가지 상태를 변화시키면서 특정 상태의 최적해를 가지고서 현재 상태의 최적해를 구하는 점화식을 구현해서 풀었다. 하지만, 배낭 문제(KnapSack Problem) 유형이라고도 불리는 이 문제에서는 두 가지 상태를 변수로 두고, 이를 변화시키며 최적해를 찾아 나간다. 그렇기 때문에 DP 배열이 2차원 배열로 만들어지고, 2차원 DP라고도 불린다.
배낭 문제(KnapSack Problem) - 2차원 DP
배낭 문제를 처음 접하면, 어떤 상태를 변수로 둬야 할지 감이 오지 않는 경우가 많다. 이 부분에 대해서 어떻게 떠올릴 수 있을지 나름의 방법을 고민 해보고 적도록 하겠지만, 이해가 전혀 가지 않는다면 결론만 외워도 좋을 것 같다.
우리는 특정 물건들로 가방을 채워 만들 수 있는 최대 가치를 저장해야 한다. 그렇다면 우리가 특정한 상황, 즉 가방에 일부 물건이 채워진 상태에 놓여 있다고 가정해 보자. 이때 현재 가방에 담긴 가치가 최적해인지 판단하려면, 가장 먼저 남은 물건 중에서 빈 공간에 더 넣을 수 있는 물건이 무엇인지 확인하는 과정이 필요할 것이다.
여기서 우리는 힌트를 얻을 수 있다. 빈 공간에 최적의 가치를 담는 방법이 존재한다면, 이를 활용해 더 나은 결과를 만들 수 있다. 그렇기 때문에 첫 번째 상태 변수는 '가방의 최대 무게'이다. 가방의 최대 무게를 작은 값부터 점점 증가시키면서, 특정 무게에서 만들 수 있는 최적의 가치를 저장해 두면, 이후 더 큰 무게에서도 이 값을 활용할 수 있다. 이러한 방식으로 현재 상태를 이전 상태를 기반으로 확장할 수 있게 된다.
w=0 → 배낭을 아예 사용하지 않은 상태
w=1 → 최대 무게가 1 kg일 때 최적해
w=2 → 최대 무게가 2 kg일 때 최적해
…
w=K → 최대 무게가 K kg일 때 최적해
또한, 특정 물건을 가방에 담았을 때 남은 공간을 활용하려면, 이전 상태가 해당 물건을 고려하지 않은 상태여야만 한다. 즉, 현재 물건을 포함한 상태와 포함하지 않은 상태를 구분해야 한다. 이를 위해 두 번째 상태 변수로 ‘물건의 종류’를 사용한다. 특정 물건까지 고려한 경우와 고려하지 않은 경우를 따로 관리하면, 현재까지의 최적해를 저장하고 이를 바탕으로 다음 단계를 계산할 수 있다. 여기서 조금 특이한 점은 특정 물건을 고려하는 단계에서 남은 공간을 활용할 때 그 물건을 제외한 모든 물건을 고려하지는 않는다는 점이다. 두 번째 물건의 경우 남은 공간에 첫 번째 물건까지 고려한 최적해를 이용하고, 세 번째 물건의 경우 남은 공간에 두 번째 물건까지 고려한 최적해를 이용하는 방식으로 확장하더라도 결국 최종적으로는 모든 물건을 고려한 최적 상태에 도달할 수 있다는 점을 이해해야 한다.
i=0 → 아무것도 고려하지 않은 상태
i=1 → 첫 번째 물건까지 고려
i=2 → 두 번째 물건까지 고려
…
i=N → 모든 물건을 고려한 최적 상태
결국, 배낭 문제에서는 ‘가방의 무게’와 ‘현재까지 고려한 물건의 종류’를 상태 변수로 설정하는 것이 핵심이다.
문제 풀이(JavaScript, Node.js)
DP 배열 선언
const dp = Array.from({ length: N + 1 }, () => Array(W + 1).fill(0));
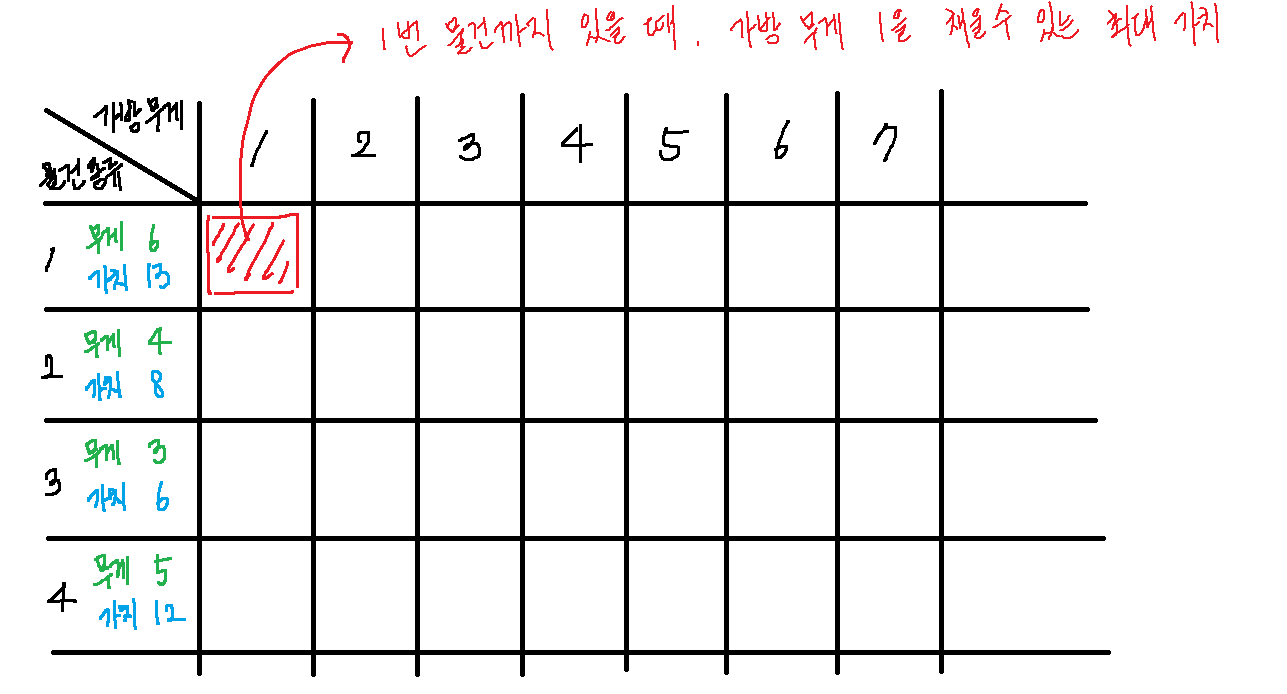
2차원 DP 배열을 선언하고, 각 칸의 값은 특정 물건(i)까지 존재할 때, 특정 가방 무게(w)를 채울 수 있는 최대 가치를 의미한다. 첫 번째 줄을 채울 때 예외처리를 따로 하지 않으려면 각각 0번째 줄(아무 물건도 없는 경우, 가방 무게가 0인 경우)을 고려해서 N+1, W+1 크기의 배열로 선언하는 것이 좋다.
DP 배열 채우기
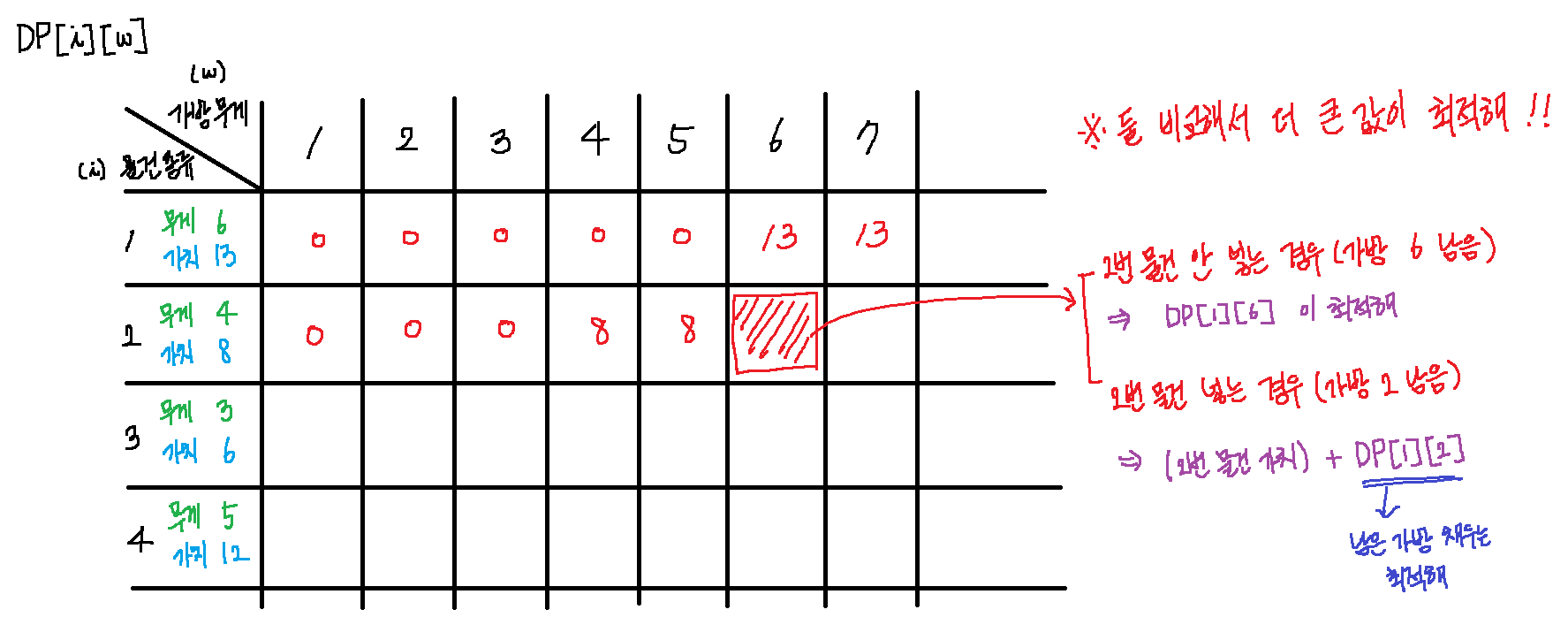
각각의 칸을 채우면서 두 가지 값을 비교 해줘야 한다.
현재 물건을 넣지 않는다면, 현재 가방 최대 무게가 그대로(w) 남게 되고, 그 남은 부분을 채울 값은 현재 물건을 고려하지 않는 시점(i-1)으로부터 가져와야 한다.
dp[i - 1][w]현재 물건을 넣는다면, 현재 가방 최대 무게에서 현재 물건의 무게 많큼 뺀 부분(w - weights[i])을 채워넣어야 하고, 마찬가지로 남은 부분을 채울 값은 현재 물건을 고려하지 않는 시점(i-1)으로부터 가져와야 한다.
values[i] + dp[i - 1][w - weights[i]]가방의 최대 무게를 고려했을 때, 현재 물건을 넣을 수 없다면 바로 전자의 값을 가져오면 되는 것이고, 현재 물건을 넣을 수 있다면 두 경우를 비교해서 더 큰 값을 최적해로 하면 된다.
// 현재 물건을 넣지 못 하는 경우(이전 최적해 그대로 가져옴)
dp[i][w] = dp[i - 1][w];
// 현재 물건을 넣을 수 있는 경우
if (w >= weights[i]) {
dp[i][w] = Math.max(dp[i - 1][w], values[i] + dp[i - 1][w - weights[i]]);
}결과
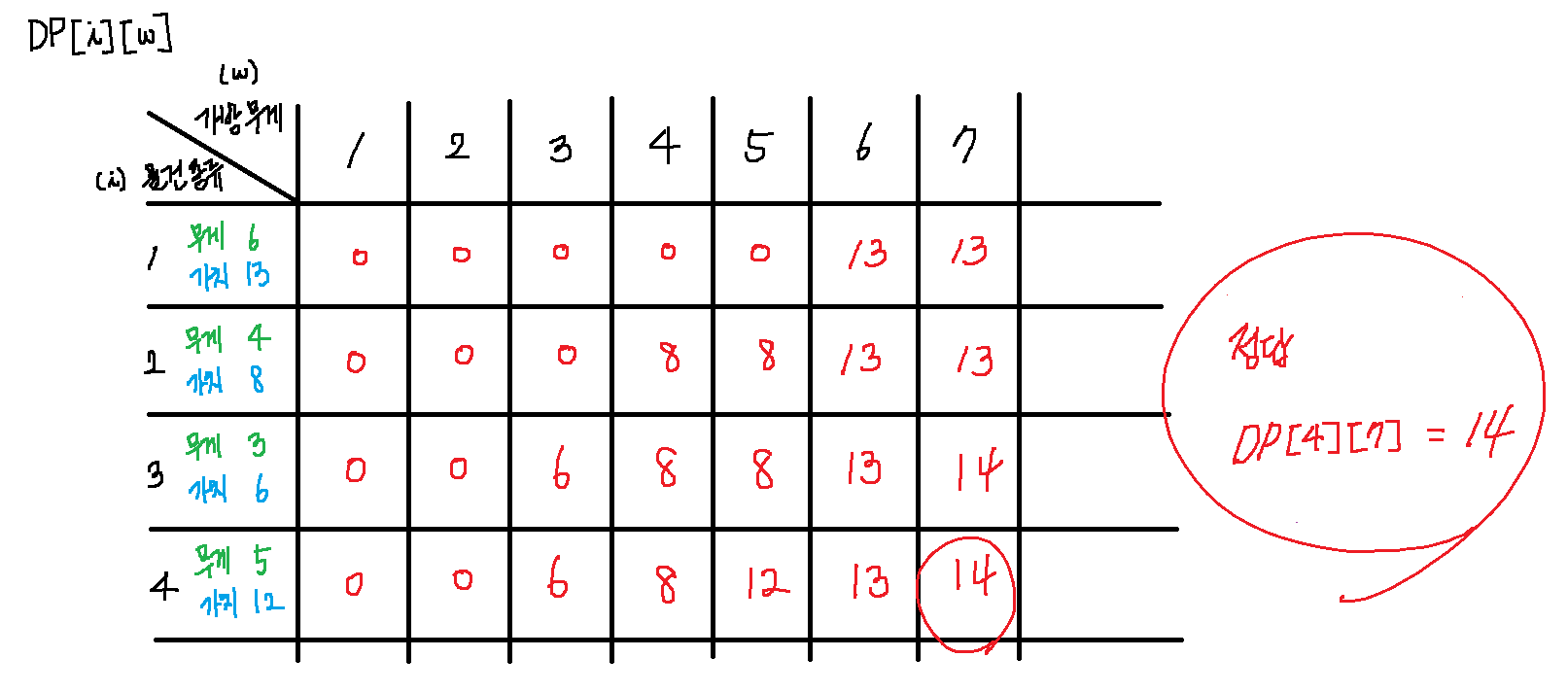
이렇게 하면, 최종적으로 다음과 같이 2차원 DP 배열을 채울 수 있다.