문제 설명
길이가 같은 배열 A, B 두개가 있습니다. 각 배열은 자연수로 이루어져 있습니다.
배열 A, B에서 각각 한 개의 숫자를 뽑아 두 수를 곱합니다. 이러한 과정을 배열의 길이만큼 반복하며, 두 수를 곱한 값을 누적하여 더합니다. 이때 최종적으로 누적된 값이 최소가 되도록 만드는 것이 목표입니다. (단, 각 배열에서 k번째 숫자를 뽑았다면 다음에 k번째 숫자는 다시 뽑을 수 없습니다.)
예를 들어 A = [1, 4, 2] , B = [5, 4, 4] 라면
- A에서 첫번째 숫자인 1, B에서 첫번째 숫자인 5를 뽑아 곱하여 더합니다. (누적된 값 : 0 + 5(1x5) = 5)
- A에서 두번째 숫자인 4, B에서 세번째 숫자인 4를 뽑아 곱하여 더합니다. (누적된 값 : 5 + 16(4x4) = 21)
- A에서 세번째 숫자인 2, B에서 두번째 숫자인 4를 뽑아 곱하여 더합니다. (누적된 값 : 21 + 8(2x4) = 29)
즉, 이 경우가 최소가 되므로 29를 return 합니다.
배열 A, B가 주어질 때 최종적으로 누적된 최솟값을 return 하는 solution 함수를 완성해 주세요.
제한 사항
- 배열 A, B의 크기 : 1,000 이하의 자연수
- 배열 A, B의 원소의 크기 : 1,000 이하의 자연수
입출력
| A | B | answer |
|---|---|---|
| [1, 4, 2] | [5, 4, 4] | 29 |
| [1, 2] | [3, 4] | 10 |
문제 이해
길이가 같은 자연수 배열이 두 개 있을 때, 각각의 배열에서 자연수를 중복되지 않게 하나씩 뽑아 곱한 값을 누적하여 더하는 간단한 문제이다.
굉장히 흔한 문제이고, 문제 풀이도 잘 알려진 문제이지만 막상 문제를 아무거나 뽑아서 풀다 보니까 처음에 그리디인지 확신을 못 하기도 했고, 그리디로 푸는 과정에서 '이렇게 정리해두면 계속해서 써먹을 수 있겠다'는 생각이 들어서 정리해놓고자 벨로그를 켰다.
접근 방법
처음에 아무 생각 없이 풀다가 누적합 조합을 다 찾으면 되나 싶은 생각에 백트래킹으로 접근을 했었다.
백트래킹
백트래킹으로 풀게 되면 최대 1000개의 길이를 가진 배열이기 때문에 A배열 1000개가 각각 B배열 1000개의 선택지를 가지기 때문에 모든 경우를 확인하기 위해서는 1000의 1000제곱이라는 어마무시한 연산횟수를 가지게 된다.
보통 백트래킹에서 실패하는 경우 DP나 그리디를 통해 접근해 보는데, 여기서는 이전의 연산 결과를 활용할 여지가 없어보여서 DP는 탈락이다.
그리디
그제서야 한 가지 아이디어가 떠올랐다. 이걸 쉽게 납득시킬 방법이 없을까 여러 가지로 고민을 해봤는데, 개인적으로 가장 쉬운 방법은 A배열과 B배열에 의미를 부여하는 방법이었다.
곱셈이라는 것은 다르게 말하면 해당 횟수만큼 반복해서 더하는 것으로 볼 수 있다. 이 때 A배열에서 뽑은 숫자를 더할 숫자라고 보고, B배열에서 뽑은 숫자를 반복해서 더할 횟수라고 생각해보자.
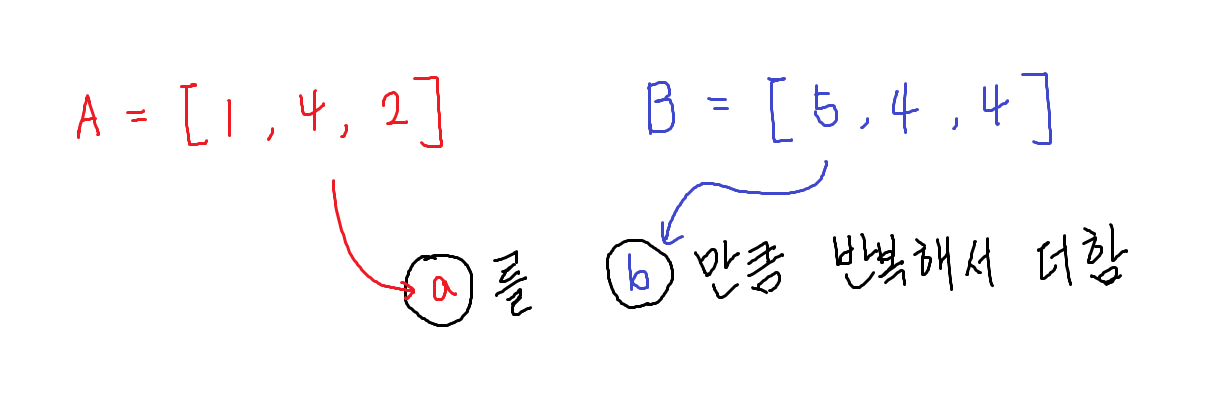
이렇게 보면 좀 더 명확하게 보이는 것 같다. 전체 누적합을 최소로 만들고 싶을 때, A에서 최솟값을 뽑았다면, 얘를 많이 더하고 싶을까? 조금 더하고 싶을까? 최소로 만들기 위해서는 최솟값을 최대한 많이 더해야 한다.
그렇기 때문에 결과적으로 매순간 A배열과 B배열에서 각각 최솟값과 최댓값을 뽑아서 곱해주면 되는 것이다. 따라서 A배열과 B배열을 반대로 정렬해두고(A가 내림차순이라면 B는 오름차순), 각각의 인덱스에 해당하는 숫자끼리 곱해서 더해주면 된다.
문제 풀이(C++)
#include <bits/stdc++.h>
using namespace std;
int solution(vector<int> A, vector<int> B) {
int answer = 0;
sort(A.begin(), A.end());
sort(B.begin(), B.end(), greater<>());
for (int i = 0; i < A.size(); i++) {
answer += A[i] * B[i];
}
return answer;
}
