문제
어떤 동물원에 가로로 두칸 세로로 N칸인 아래와 같은 우리가 있다.
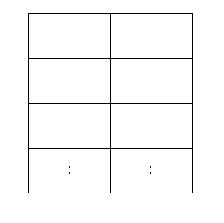
이 동물원에는 사자들이 살고 있는데 사자들을 우리에 가둘 때, 가로로도 세로로도 붙어 있게 배치할 수는 없다. 이 동물원 조련사는 사자들의 배치 문제 때문에 골머리를 앓고 있다.
동물원 조련사의 머리가 아프지 않도록 우리가 2*N 배열에 사자를 배치하는 경우의 수가 몇 가지인지를 알아내는 프로그램을 작성해 주도록 하자. 사자를 한 마리도 배치하지 않는 경우도 하나의 경우의 수로 친다고 가정한다.
문제 분석
-
2 * N 사이즈의 우리에 사자들 배치
-
사자들을 가로로도 세로로도 붙어 있게 배치할 수는 없다.
-
배치할 수 있는 경우의 수 구하기
-
한 마리도 배치하지 않는 경우도 한 가지 경우의 수에 해당
접근 방법
나는 우선 경우의 수 문제를 보면 완전탐색 혹은 DP를 생각해두는데, 우선 완전탐색을 했을 경우에 시간복잡도를 어림잡아 계산 해보고, 이건 아니다 싶으면 DP를 선택하는 것 같다.
이 문제의 경우는 N이 10만일 경우 20만 개의 칸이 있고 각각의 칸에 사자를 넣거나 안 넣을 수 있으니 총 경우의 수가 2의 20만 제곱이 나오는 것 같아서, DP로 풀어야 하는구나 생각했다.
DP 문제는 항상 느끼는 것이 펜을 들게 만드는 것 같다. 마냥 문제만 들여다보고 있으면 규칙이 잘 보이지는 않는 것 같아서 써 보면서 규칙을 찾는 편이다.
손으로 써보기
규칙을 찾으려고 손으로 써 본 것도 있지만 '가로로도 세로로도'의 의미가 명확한 것 같지 않아서 써본 것도 있다. 특정 칸을 기준으로 가로와 세로에 동시에 붙어 있으면 안된다는 것인지 둘 중 하나만 붙어 있어도 안된다는 것인지 애매해서 예제 케이스를 손으로 써 보았다.
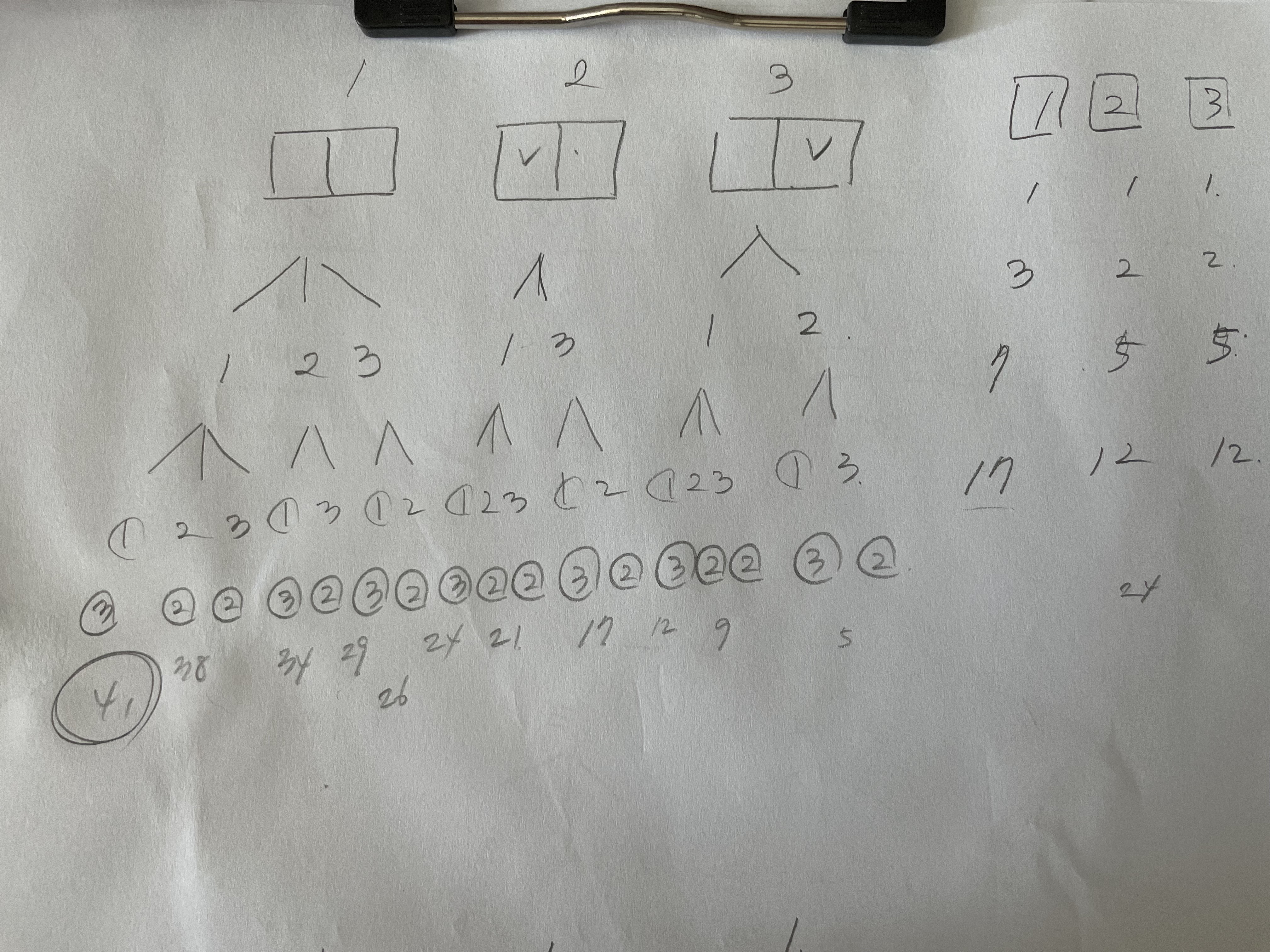
처음에 가로와 세로에 동시에 붙어 있으면 안된다는 의미로 계산 해봤더니 경우의 수가 너무 많이 나왔고, 둘 중 하나만 붙어 있어도 안된다는 의미로 계산 해보니 예제 정답과 똑같이 나왔다. 손으로 써 보면서 규칙을 찾게 되었는데, 이제 저 필기의 의미를 해석해보도록 하자.
문제 풀이
1. 한 줄에 배치할 수 있는 경우의 수
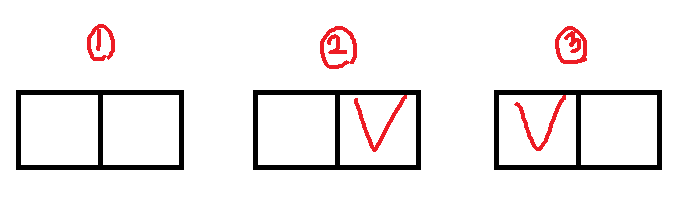
한 줄에 사자를 배치할 수 있는 경우는 총 세 가지다. 한 마리도 안 넣거나, 오른쪽에 한 마리 혹은 왼쪽에 한 마리를 배치할 수 있다. 각각의 경우에 1번, 2번, 3번 번호를 붙여두자.
2. 다음 줄과의 관계
-
1번
윗 줄이 1번과 같은 빈 줄이었다면, 다음 줄에 올 수 있는 경우는 1번, 2번, 3번 세 가지 경우가 올 수 있다. -
2번
윗 줄이 2번이었다면, 똑같은 2번과 같은 경우를 제외하고 1번, 3번 두 가지 경우가 올 수 있다. -
3번
마찬가지로 윗 줄이 3번이었다면, 똑같은 3번과 같은 경우를 제외하고 1번, 2번 두 가지 경우가 올 수 있다. -
수형도(나뭇가지 그림)
위 그림을 수형도를 이용해서 그려보면 아래 그림과 같이 나타낼 수 있고, 맨 아랫줄의 경우를 다 세어주면 총 경우의 수가 된다.
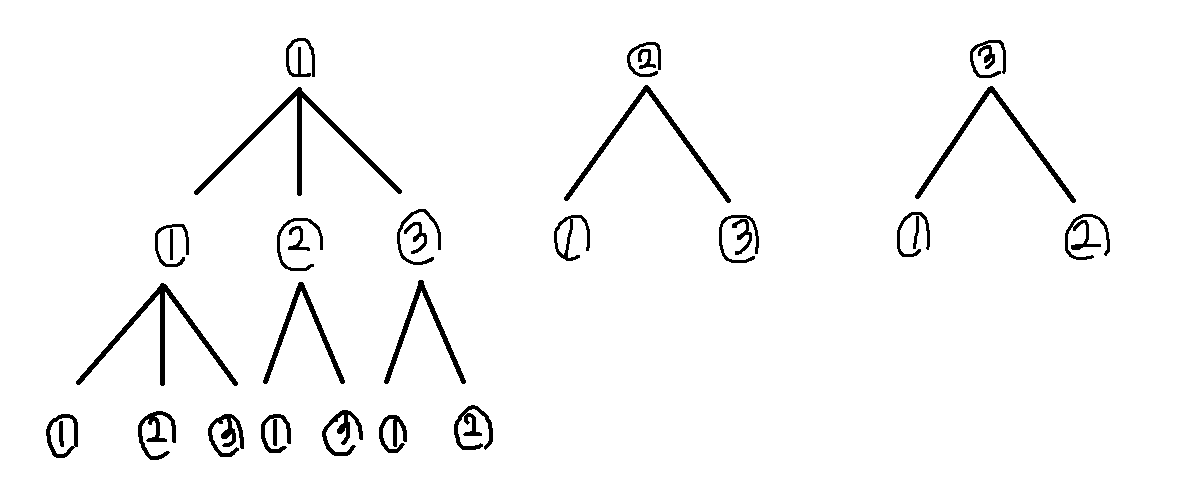
-
점화식
윗 줄의 1번, 2번, 3번의 개수를 알고 있으면 다음 줄의 1번, 2번, 3번의 개수를 알아낼 수 있다.- (1번 개수) = (윗 줄의 1번 개수) + (윗 줄의 2번 개수) + (윗 줄의 3번 개수)
- (2번 개수) = (윗 줄의 1번 개수) + (윗 줄의 3번 개수)
- (3번 개수) = (윗 줄의 1번 개수) + (윗 줄의 2번 개수)
와 같이 나타낼 수 있고, 마지막 줄의 1번, 2번, 3번 개수를 다 더하면 총 경우의 수를 구할 수 있다.
코드(C++)
#include <bits/stdc++.h>
using namespace std;
int main() {
int N = 0;
vector<pair<pair<int, int>, int>> DP;
cin >> N;
DP.push_back({{1, 1}, 1});
for (int i = 0; i < N; i++) {
int x, y, z;
x = (DP[i].first.first + DP[i].first.second + DP[i].second) % 9901;
y = (DP[i].first.first + DP[i].second) % 9901;
z = (DP[i].first.first + DP[i].first.second) % 9901;
DP.push_back({{x, y}, z});
}
cout << (DP[N-1].first.first + DP[N-1].first.second + DP[N-1].second) % 9901;
return 0;
}글을 마치며
요즘 자소서나 네부캠이나 너무 정신이 없어서 포스팅할 시간이 없었다고 변명은 해보지만... 길게 쓰진 않더라도 짧은 글이라도 꾸준히 내 생각을 기록하는 습관을 들여봐야겠다!! 다음주부터 네이버 부스트캠프 챌린지 과정에 들어가는데, 챌린지 과정에서 공부하는 것들을 회고하는 방식으로 포스팅 해봐야겠다!!

