https://openreview.net/pdf?id=k38Th3x4d9

Introduction

• 다변량 시계열 데이터에 대한 root cause는 이상 현상의 근본 원인을 식별하는 것으로, 온라인 클라우드 기반 또는 사이버 물리 시스템의 결함 진단과 같이 다양한 도메인에서 광범위한 응용 분야를 가짐
• 시스템의 topology를 기반으로 근본 원인을 수동으로 추적하는 기존 접근법은 시스템 복잡성 증가로 인해 비현실적이 되었으며, 데이터 기반 방법에 대한 관심이 높아지게 되었고, 유망한 방향 중 하나는 causal framework에 기반한 것으로, causal graph를 통해 시스템 구성 요소와 그 의존성을 모델링한 다음 한 구성 요소의 failure가 시스템을 통해 어떻게 전파될 수 있는지 추적하는 것임
• 하지만 기존의 인과 추론 방법은 대부분 causal relationship 구조를 사전에 알거나 기존 인과 발견 알고리즘을 활용하는 데 그쳐, 실제 root cause 탐지에는 한계가 있음
• 이에 본 논문은 Granger causality 탐색과 root cause 분석을 통합한 새로운 접근법인 AERCA를 제안함

---

Related Work

Traditional approaches

• 초기에는 도메인 지식이나 시스템 호출 로그와 같은 정보를 활용하여 변수들 간의 의존성 그래프를 구축하는 방법을 주로 사용하였음
• 하지만 시스템이 점점 복잡해짐에 따라 수작업이나 호출 로그만으로는 실제 인과 관계를 정확히 반영하기 어려움

Data-driven approaches / causal inference-based approaches

• 위 문제를 해결하기 위해 최근에는 데이터에서 직접 causality graph를 학습하는 머신러닝 알고리즘들이 활발히 개발됨
• 다양한 신경망 구조를 이용해 시계열 변수 간의 causal relationship을 탐색하고 이를 root cause 분석에 적용하는 연구들이 진행되었음
• 특히 인과 추론을 통해 이상을 외부 개입으로 보고, 개입된 노드를 찾아내는 방법들이 주목받고 있음

→ 기존의 인과 추론 기반 방법들은 다음과 같은 한계를 가짐

1. 인과 구조를 사전에 알고 있어야 하는 경우가 많아 현실 적용이 제한적임
2. 인과 발견 알고리즘을 그대로 사용해 root cause 탐지 목적을 명확히 반영하지 못함
3. 외생 변수(exogenous variables)의 영향이나 개입을 명시적으로 모델링하지 않아 이상이 발생한 시간 단계나 특정 원인 변수의 위치를 정확히 찾기 어려움

---

Preliminary: Granger Causality

Granger causality는 다변량 시계열 데이터에서 causal relationships를 모델링하는 데 자주 사용됨.

시계열 $X$의 과거 데이터가 시계열 $Y$의 미래 값을 예측하는 데 영향을 미친다면 $X$가 $Y$를 “Granger cause”한다고 할 수 있으며, 초기에는 선형 관계에 대해 정의되었지만 최근에는 비선형 관계에 대해서도 연구되며, 이는 복잡한 인과 관계를 분석하는 데 도움을 줌.

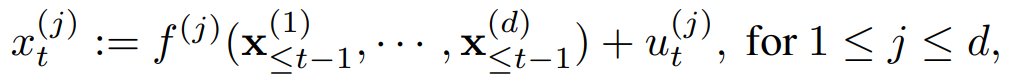
여기서 $x_t^{(j)}$는 $j$번째 시계열의 $t$ 시점 값이고, $f^{(j)}(·)$는 $j$번째 시계열의 현재 값에 영향을 주는 과거 시계열들의 함수이고, $u_t^{(j)}$는 외생변수로, 인과 구조 밖에서 발생하는 변수이다.

만약 $f^{(j)}$ 함수에 시계열 $i$의 과거가 포함되어 있다면, 이는 시계열 $i$가 $j$를 Granger cause 한다고 말할 수 있다.

하지만 Granger causality의 한계는 숨겨진 교란 변수(hidden cofounders)의 부재를 가정하며, 변수 간 즉각적 영향(instantaneous effects)이 없음을 가정함.

---

Methodology

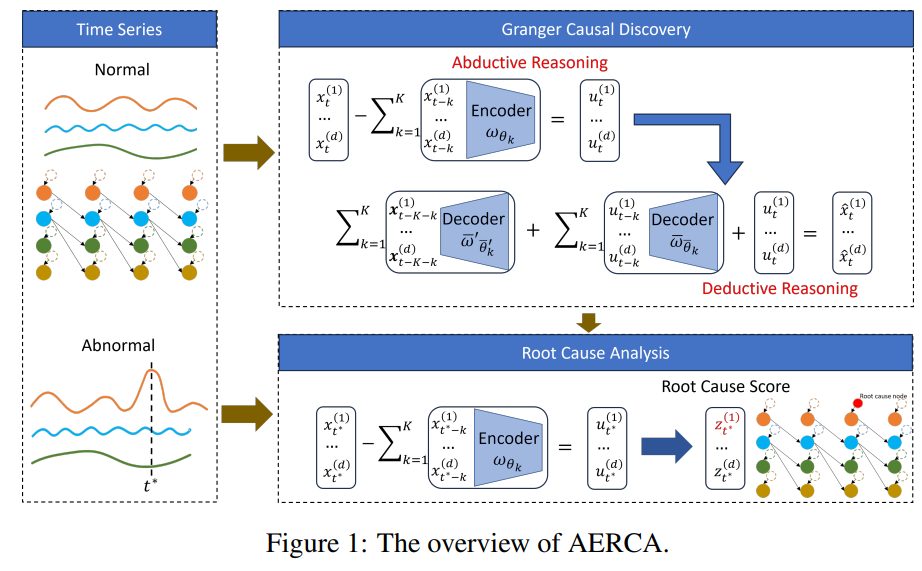
Problem Formulation and Framework

다변량 시계열 구조 방정식에 기반하여, 본 연구는 외생 변수의 개입이 발생한 경우의 이상 $\tilde x_t^{(j)}$에 초점을 맞춘다. 이는 정상 상태의 함수 $f^{(j)}(x^{(1)}_{\le t-1}, ..., x^{(d)}_{t-1})$에 외생 변수 $\hat u_t^{(j)}$가 더해진 형태로 표현된다:

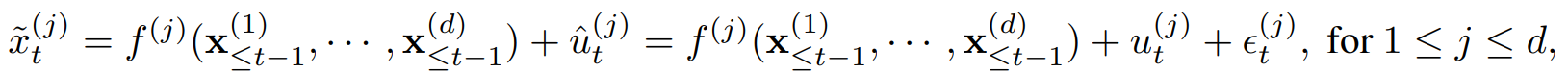
여기서 $\epsilon_t^{(j)}$은 anomaly term이다.

이러한 외생 변수의 개입은 특정 시점에 한 시계열에서 발생하는 point anomaly일 수도 있고, 시간에 걸친 연속적인 개입으로 인한 sequential anomaly일 수도 있다. 본 연구에서 문제로 삼는 것은 단순히 이상을 탐지하는 것이 아니라, 이상이 발생한 특정 시계열 변수와 그 발생 시간 시점까지 효과적으로 식별하는 것이다.

외생적 개입으로 인한 이상 현상에 대해 근본 원인 분석을 달성하기 위해, 저자들은 외생 변수의 분포를 명시적으로 모델링하여 다변량 시계열에서 Granger causality를 학습하고자 AERCA라는 root cause analysis를 위한 encoder-decoder 구조를 개발하며, 이는 특정 시점의 각 시계열에 대한 외생 변수를 계산할 수 있다.

Granger Causal Discovery

Motivation

외생 변수의 분포뿐만 아니라 데이터 생성 프로세스, 즉 인과 관계를 모델링하기 위해, 저자들은 귀추적(abductive) 및 연역적(deductive) 추론 프로세스를 모두 시뮬레이션하기 위해서 encoder-decoder 구조를 채택한다.

귀추적 추론은 가장 그럴듯한 설명을 찾는 것, 즉 관찰된 시계열 데이터를 생성했을 가능성이 가장 높은 외생 변수(원인)을 추론하는 것이다.

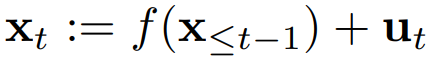
위 식에서 볼 수 있듯이, Granger causality에 기초하여 단계 $t$에서의 시계열 값은 과거 시계열의 함수에 현재 단계에서의 외생적 항을 더한 값이다. 귀추적 추론을 시뮬레이션하기 위해, encoder는 위 식을 아래와 같이 재작성하여 관찰된 데이터를 기반으로 외생 변수를 도출한다.

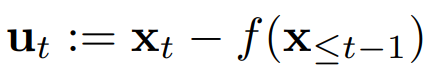
반면, 연역적 추론은 알려진 원인으로부터 결과를 도출한다. 즉, 외생 변수로부터 관찰된 데이터를 재구성한다. 각 이전 시간 단계를 재귀적으로 해결함으로써 위 식을 아래와 같이 재작성할 수 있다.

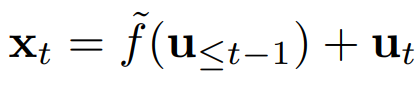
이는 단계 $t$에서 관찰된 데이터가 모든 이전 외생 변수의 함수 $\tilde f(·)$로 표현됨을 보여주고, 이 함수는 encoder-decoder 구조 내에서 외생 변수로부터 직접 관찰된 데이터를 재구성하기 위한 decoder 역할을 한다. 이러한 분석을 바탕으로 encoder가 과거 시계열 값을 입력으로 사용하여 외생 변수를 계산하여 Granger causal 관계 $f(·)$를 학습하는 encoder-decoder 구조를 개발한다.

Encoder-decoder Structure

Data preparation

정상 다변량 시계열 $X = (x_1, …, x_t, …,x_T)$가 주어졌을때, 길이가 $K$인 윈도우를 $W_t = (x_{t-K+1},...,x_t)$로 정의하고 시계열 $X$를 슬라이딩 윈도우 시퀀스 $\mathcal W = (W_K, W_{K+1}, …, W_T)$로 변환한다. 이후 먼저 window causal graph를 학습하여 윈도우 내 Granger causality를 학습하게 된다.

먼저 시계열의 Granger causality를 다음과 같이 파라미터화 한다:

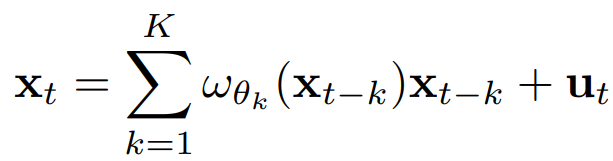
여기서 $\omega_{\theta_k}(x_t-k)$는 $x_{t-k}$와 $x_t$ 사이의 Granger casuality 관계를 예측하는 $k$번째 신경망이다.

Encoder

$\omega_{\theta_k}(x_t-k)$의 출력은 $d \times d$ 계수 행렬로 재구성될 수 있으며, 여기서 엔트리 요소 $(i, j)$는 $x_{i-k}^{(j)}$가 $x_t^{(i)}$에 미치는 영향을 나타낸다. 위 식에서 볼 수 있듯, $K$개의 신경망이 과거 $K$개의 time lag의 가중치를 예측하는 데 사용된다. 따라서 $K$개의 계수 행렬을 검사하여 $K$개의 time lag에 걸쳐 $d$개의 시계열 간의 관계를 탐색할 수 있다. 이제 위 식을 변형하여 외인성 변수 $u_t$를 다음과 같이 다시 쓸 수 있다:

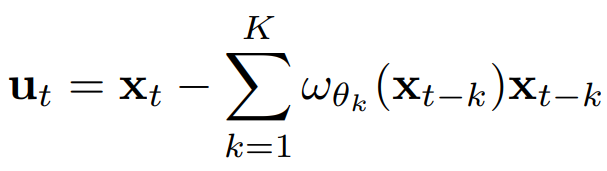
주어진 time window $W_t = (x_{t-K+1},...,x_t)$에 대해, 인코더는 이 과정을 $K$번 적용하여 윈도우 내의 외인성 변수들 $U_t = (u_{t-K+1},…,u_t)$를 추론한다. (귀추적 추론)

인코더가 추정한 윈도우 내의 외생변수들 $U_t = (u_{t-K+1}, \dots, u_t)$이 서로 독립적인 표준 정규 분포(평균 0, 공분산 행렬 I)를 따르도록 제약을 가한다. 이는 KL divergence를 이용하며, $u_t$ 벡터 내의 각 차원(즉, 각 시계열의 외생변수)이 서로 독립임을 강제하는데, 이는 구조적 인과 모델의 중요한 가정 중 하나이다.

Decoder

디코더는 외인성 변수로부터 관찰 데이터를 재구성하는 연역적 과정을 모델링한다. 이론적으로는 $x_t = \bar f(u_{\le t-1}) + u_t$처럼 모든 과거 외인성 변수를 사용해야 하지만, 무한한 길이의 시계열에서는 모든 외인성 변수를 사용하는 것이 비현실적이다. 따라서 proposition 1에 기반하여(논문 원문 참고), 디코더는 현재 값 $\hat x_t$를 재구성한다.

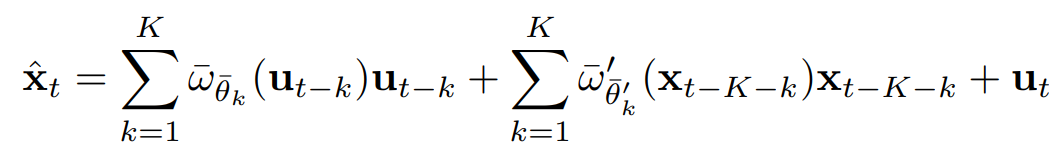
여기서,

• $\hat x_t$: 현재 시간 $t$의 $d$차원 시계열 벡터 재구성값
• $u_{t-k}$: 인코더에 의해 계산된 지연 시간 $k$만큼 떨어진 과거의 외인성 변수
• $\bar \omega_{\bar \theta_k}(·)$: 외인성 변수 $u_{t-k}$가 $\hat x_t$에 미치는 영향을 모델링하는 신경망 ($K$개)
• $x_{t-K-k}$: 시간 지연 $K + k$만큼 떨어진 과거의 관찰된 시계열 값
• $\bar \omega'_{\bar \theta_k}(·)$: 관찰된 시계열 $x_{t-K-k}$가 $\hat x_t$에 미치는 영향을 모델링하는 신경망 ($K$개)
• $u_t$: 현재 시간 $t$의 외인성 변수

요약하면, AERCA는 정상 시계열 데이터에 대해 이러한 encoder-decoder 구조를 학습시키는데, 학습 과정에서 encoder는 Granger causality relationship $\omega_{\theta_k}$를 학습하여 외인성 변수 $u_t$를 정확하게 추론하도록 하고, decoder는 추론된 외인성 변수와 과거 관찰 데이터를 사용하여 원래의 시계열 데이터 $x_t$를 잘 재구성하도록 한다.

Objective function

전체 encoder-decoder 구조는 $\hat x_t = AE_{\theta_k, \bar\theta_k, \bar \theta'_k} (x_{<t})$로 정의될 수 있으며, 길이가 $T$인 시계열이 주어졌을 때, encoder 신경망 $\omega_{\theta_k}$와 decoder 신경망 $\bar \omega_{\bar \theta_k}, \omega'_{\bar \theta'_k}$를 학습하기 위한 목적 함수는 다음과 같이 정의된다.

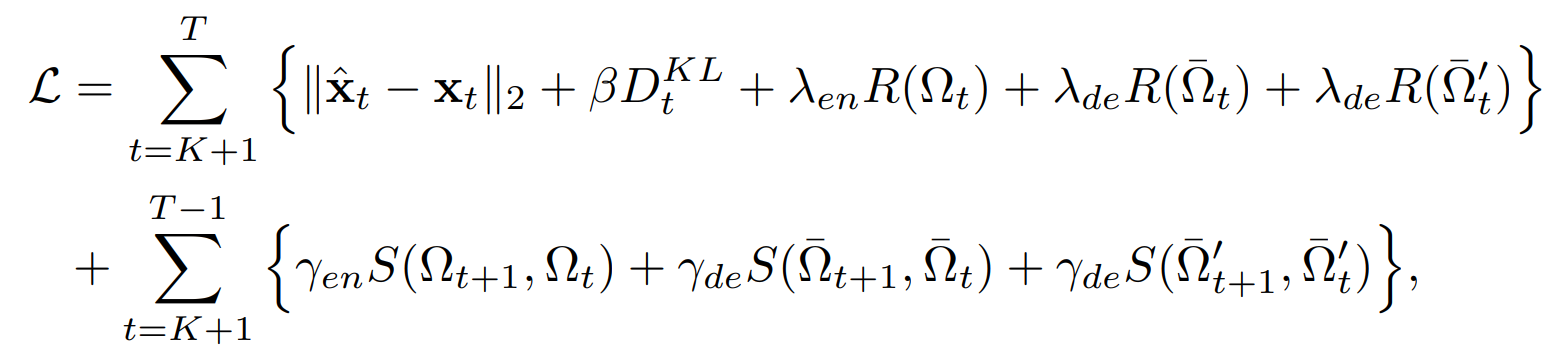
여기서,

• $||\hat x_t - x_t||_2$: 재구성 손실
• $\beta D_t^{KL}$: 외인성 변수의 독립성 제약에 대한 KL divergence term
• $\lambda_{en}R(\Omega_t)$: Encoder의 계수 행렬 $\Omega_t$에 대한 정규화 term
• $\lambda_{de}R(\bar \Omega_t)$: Decoder에서 외인성 변수의 영향을 모델링하는 계수 행렬 $\bar \Omega_t$에 대한 정규화 term
• $\lambda_{de}R(\bar \Omega'_t)$: Decoder에서 관측된 시계열 변수의 영향을 모델링하는 계수 행렬 $\bar \Omega'_t$에 대한 정규화 term
• $\gamma_{en}, \gamma_{de}$: 평활성 penalty의 중요도를 조절하는 하이퍼파라미터
• $S(·,·)$: 평활성 penalty 함수로, 연속된 시간 단계의 계수 행렬 사이의 L2 norm 차이를 측정한다. 이 term을 최소화하여 시간의 흐름에 따라 학습된 인과 관계가 급격하게 변하지 않고 부드럽게 유지되도록 한다.

Granger Causal Discovery

학습이 완료되면, encoder의 첫 번째 부분인 $w_{\theta_k}(x_{t-k})$ 신경망이 학습한 계수 행렬들을 분석하여 Granger causality를 도출한다.

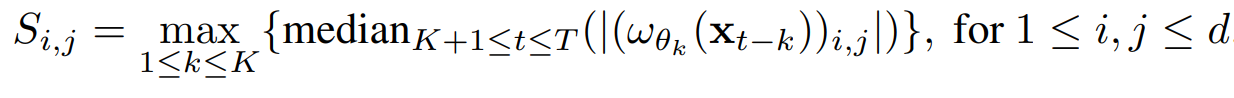
이를 바탕으로, 인접 행렬 $A$를 만든다. 특정 threshold $\tau$를 설정하여, $S_{i,j} > \tau$이면 $A_{i,j} = 1$로 설정된다.

Root Cause Localization

정상 시계열에 대해 학습한 후, 외생 변수가 encoder에 의해 근사될 수 있다고 보이고, root cause localization을 위해 모델을 배포할 때 시계열이 streaming 방식으로 도착한다고 가정하고, 아래와 같은 순서로 localization을 수행한다.

• 새로운 time step $t^*$가 도착하면 먼저 encoder를 사용하여 해당 시점의 외인성 변수 $u_{t^*}$를 계산한다.
• 각 시계열 변수 $j$에 대해 계산된 외인성 변수 값 $u_{t^*}^{(j)}$가 정상 상태에서의 외인성 변수 분포로부터 얼마나 크게 벗어나는지를 나타내는 z-score를 계산한다.
  • 이 z-score가 해당 시계열 변수 및 시점에 대한 root cuase score가 되고, z-score가 높을수록 해당 시계열 변수 및 시점이 이상의 root cause일 가능성이 높다고 판단한다.

---

Experiments

Experimental Setup

Datasets

네 가지 합성 데이터 셋(Linear Dataset, Nonelinear Dataset, Lotka-Volterra, Lorenz 96)과 두 가지 real-world 데이터 셋(SWaT, MSDS)으로 평가를 수행한다. 합성 데이터 셋은 이상 징후의 근본 원인 뿐 아니라, 구조적 인과 모델에 대한 ground truth가 존재하기 때문에 이에 대한 평가가 가능하고, real-world 데이터셋은 근본 원인 변수에 대한 정보만 있기 때문에 근본 원인 식별을 평가하는 데만 사용한다.

Evaluation Metrics

• Causal discovery: 학습된 causal graph가 ground truth와 얼마나 일치하는 지 평가
  • F1-score, AUC-ROC, AUC-PR, Hamming Distance
• Root cause identification: 이상 징후의 근본 원인이 되는 시계열 변수 및 time step을 얼마나 정확하게 찾아내는지 평가
  • AC@K: 전체 시계열 데이터 내에서 상위 K개의 root cause score를 가진 변수 목록에 실제 root cause variable이 포함될 확률을 측정
  • AC*@K: 특정 시간 단계에서의 root cause 식별 성능을 정량화하기 위해 도입된 지표로, 이 값이 높을수록 모델이 계산한 시간 단계별 root cause score가 실제 근본 원인 변수들을 효과적으로 상위 순위로 밀어올린다는 것을 의미함. → root cause variable 뿐 아니라, 이상 발생 시점을 찾는 능력까지 보게 된다.

Experimental Results

Performance of Causal Discovery

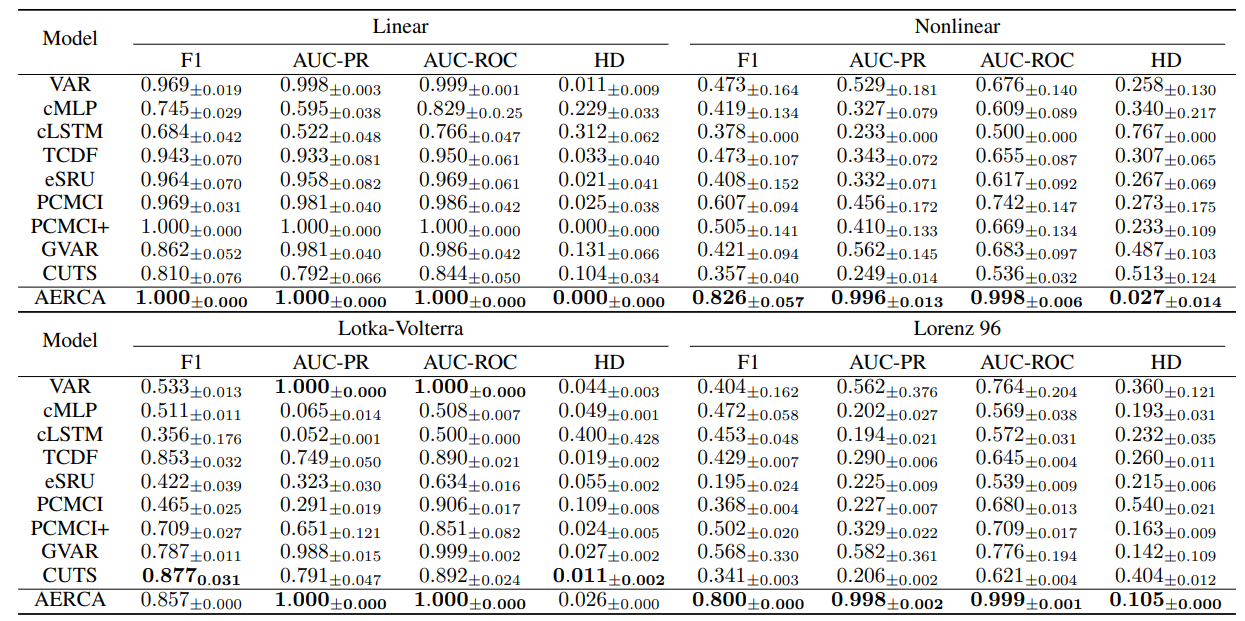
• AERCA는 Linear dataset에서 완벽한 성능을 달성하였음
• 이보다 복잡한 nonlinear dataset에서도 다른 baseline 모델들에 비해 높은 점수와 낮은 HD를 기록하며 뛰어난 성능을 보였는데, 이는 AERCA가 비선형 인과 관계를 효과적으로 발견할 수 있음을 시사한다.
• baseline 모델들은 데이터 셋 특성에 따라 성능 편차가 컸음

performance of Root Cause Identification

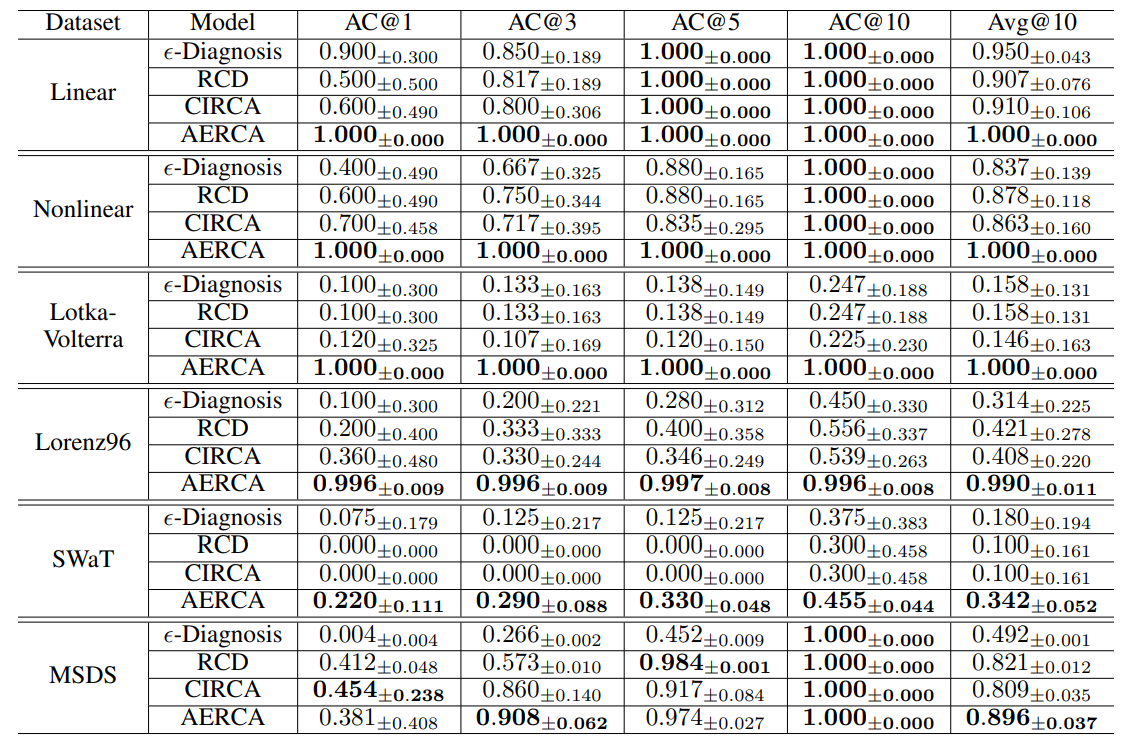
• AERCA는 SWaT 데이터셋을 제외한 대부분의 데이터셋에서 AC@1을 제외한 모든 AC@K 지표에서 1.0 또는 그에 가까운 높은 성능을 보인다. 이는 AERCA가 가장 높은 root cause score를 가진 시계열을 정확하게 식별하였다는 것을 보여준다.
• SWaT 데이터의 경우, 독립성과 같은 가정 위반과, hidden cofounder 및 instantaneous effect를 포함한 복잡한 인과 관계의 존재로 인해 모든 방법의 성능이 저하되었지만, AERCA는 baseline 방법에 비해 root cause time series를 훨씬 높은 정확도로 일관되게 식별한다.

Performance of Root Cause Analysis at Specific Time Steps

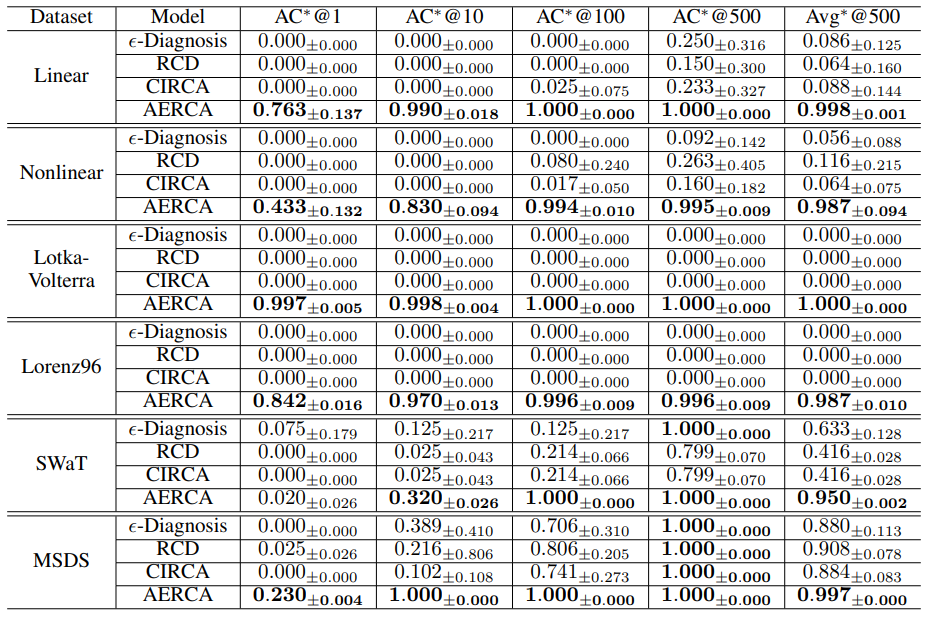
• AC@K는 기존 baseline들과 비교했을 때 AERCA의 성능이 월등히 높음을 보여준다. 특히, AC@1과 같은 낮은 K 값에서도 월등히 높은 값을 보여주는데, 이는 AERCA가 root cause variable 뿐 아니라, 특정 time step까지 정확하게 찾아내는 능력이 뛰어남을 의미한다.

Sensitivity Analysis

이상 징후의 근본 원인이 되는 외부 개입이 특정 시점 한 번으로 끝나는 것이 아니라, 여러 시점에 걸쳐 연속적으로 발생할 경우 AERCA의 성능이 얼마나 잘 유지되는지 확인

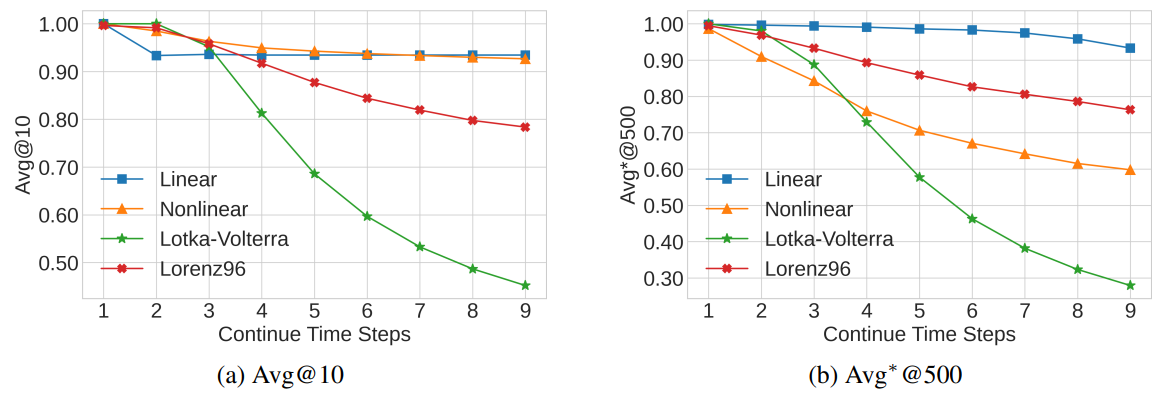
• Avg@10: Linear 및 Nonlinear 데이터셋에서는 연속적인 외부 개입 시점 수가 증가해도 AERCA의 성능이 안정적으로 유지되었음. Lotka-Volterra에서는 약간 감소하는 경향을 보였는데, 이는 AERCA가 연속적입 개입 상황에서도 root cause time series를 잘 식별하였음을 시사함
• Avg@500: Linear, Nonlinear, Lorenz96 데이터셋에서 합리적인 수준의 성능을 보였음.
  • Lotka-Volterra에서의 성능 저하의 원인은 해당 데이터 셋의 변수 수가 다른 데이터 셋보다 많아, 특정 시간 단계에서의 root cause 후보가 기하급수적으로 늘어나기 때문으로 분석한다.

Case Study

Nonlinear 데이터 셋의 짧은 다변량 시계열 snippet을 사용하여 4개의 다른 시계열에 걸쳐 다른 time step 4개의 외인성성 개입을 인위적으로 주입하였음(Ground Truth). 보라색 막대는 AERCA가 root cause score가 가장 높은 상위 5개로 예측한 부분

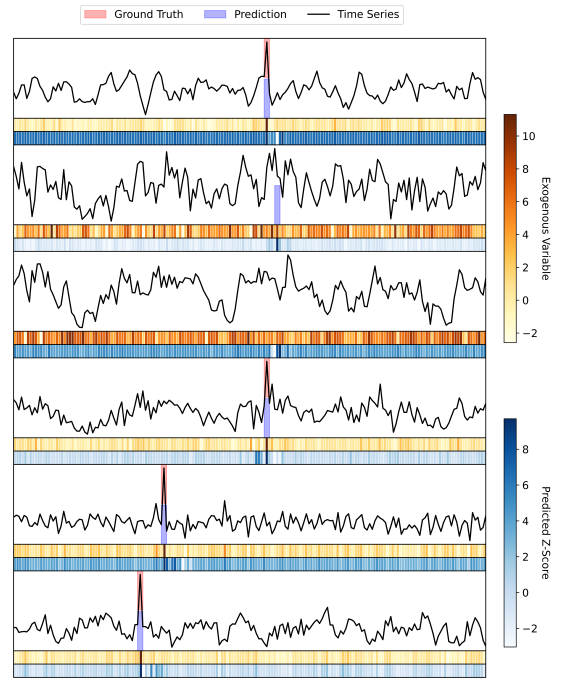
• AERCA는 외부 개입이 발생한 특정 시점에서 root cause 시계열 변수를 정확하게 감지하였음
• 계산된 z-score가 실제 외부 변수의 패턴과 잘 일치함을 보여주며, 특히 외부 개입이 발생했을 때 이 일치성이 두드러짐. 이는 AERCA가 외부 변수의 이상을 효과적으로 포착함을 의미함.

Ablation Study

외생 변수를 적절하게 학습하려면 서로 다른 시계열의 외생 변수가 서로 독립적인지를 확인하는 것이 중요하다. 학습 과정에서 외생 변수에 대한 독립 제약 조건을 제외하고 ablation 실험을 진행한 결과는 아래와 같다.

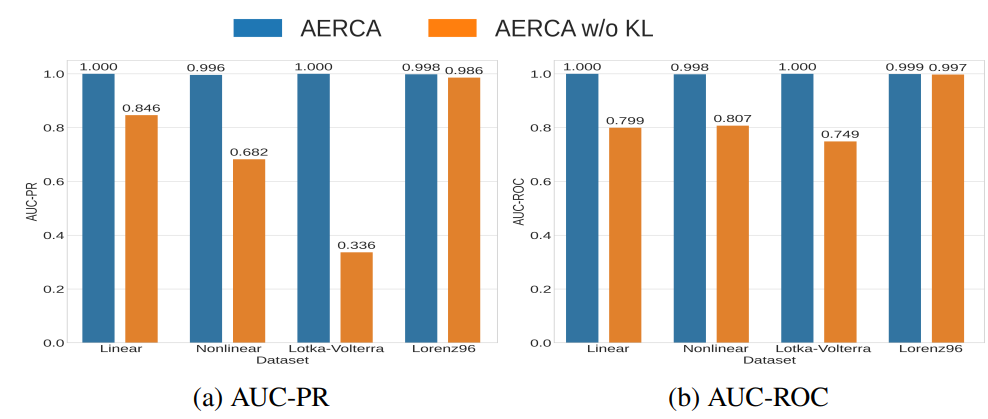
• 위 그래프에서 확인 가능하듯이, Lorenz96 데이터를 제외하고는 외인성 변수에 대한 독립성 제약을 objective function에서 제외하고 AERCA의 causality relationship discovery 발견 성능이 훨씬 낮아지는 것을 확인할 수 있다.
• Lorenz96에서도 미미하긴 하였지만, 성능 하락이 이어졌다.