[논문 리뷰] GCAD: Anomaly Detection in Multivariate Time Series from the Perspective of Granger Causality (AAAI 2025)

shyoon·2025년 7월 7일
Anomaly DetectionTime Series논문리뷰딥러닝머신러닝
0

논문리뷰

목록 보기
22/27

https://arxiv.org/html/2501.13493v1

Introduction

  • 시계열 데이터는 물 공급 시스템, 항공 우주 및 서버 시스템과 같은 많은 산업 시스템에서 생성됨. 이러한 시스템은 복잡한 내부 의존성과 비선형 관계를 나타내는데, 관련 분야의 급속한 발전으로 인해 센서에서 생성된 대량의 모니터링 데이터에서 시스템 이상을 발견하는 것이 중요한 문제가 되었음.
  • 최근 Graph Neural Network (GNN)은 변수 간의 공간적 의존성을 효과적으로 포착하여 시계열 이상 탐지에서 큰 잠재력을 보여주었는데, 기존 방식은 그래프를 학습한 후 재구성 또는 예측 오차를 기반으로 이상 탐지를 수행하였는데, 이는 시계열 임베딩 벡터 간의 유사성만 학습할 뿐, 그래프가 시계열 진화에 미치는 역할에 대한 해석력이 부족함. 실제 이상은 종종 의존성 구조의 변화를 동반하게 됨.
  • 따라서 인과관계가 해석 가능한 의존성 구조 학습이 이상 탐지에 효과적이나, 현실 시스템은 복잡하고 많은 비선형성이 존재하여 데이터 기반으로 해석 가능한 관계 학습이 어려움.
  • 이를 해결하기 위해 본 논문에서는 Granger Causality-based multivariate time series Anomaly Detection method (GCAD)를 제안

Related Works

Multivariate Time Series Anomaly Detection

  • 초기 방법들은 ARIMA와 같은 통계 기반 모델에 집중하였음
  • 최근에는 딥러닝 기법들이 널리 활용되고 있으며, 이는 비선형 관계를 효과적으로 학습하지만, 기존 방법들은 변수들 간의 공간적 종속성을 명시적으로 잘 모델링 하지 못하였음
  • GNN은 변수 간 공간적 종속성을 모델링하는 데 유용하며, 그래프 구조가 없는 경우 adaptive graph learning module을 통해 학습함.
    • 하지만 기존 GNN 기반 방법들은 공간적 종속성 패턴을 이상 탐지에 직접 적용하지는 않았음

Inter-sequence Correlations Modeling

  • 대부분의 GNN 기반 방법(VGCRN, FuSAGNet)은 임의로 초기화된 임베딩 벡터를 사용하여 고정된 그래프 구조를 구성하며, 이를 통해 공간적 의존성을 모델링함
    • 하지만 downstream task를 기반으로 하는 최적화 방법은 안정적이고 의미 있는 그래프 구조를 생성하지 못할 수 있음
  • Self-attention 기반 방법들은 동적으로 각 시점에 맞는 그래프 구조를 생성할 수 있으나, 무작위로 초기화된 attention network 때문에 실제 의미 있는 공간 관계를 학습하지 못할 수 있음
  • 과거 연구들은 간단한 선형 통계 모델에 기반한 Granger causality를 이용해 시퀀스 간 공간 관계를 모델링하려 하였으나, 복잡한 비선형 의존성은 설명하지 못함

Methodology

Problem Statement

본 논문에서는 다변량 시계열에서의 anomaly detection task를 조사함. 본 연구의 다변량 시계열 데이터는 실제 시스템의 다양한 센서에서 수집되었으며, 일정한 간격으로 일정 기간 동안 관찰됨.

관찰된 시계열은 {x1,x2,...,xT}\{x_1, x_2, ..., x_T\}와 같은 time point 집합으로 나타낼 수 있으며, 여기서 xt∈RNx_t \in \mathbb R^N은 시간 tt에서 NN개의 센서에서 얻은 관측값을 나타냄.

Anomaly detection task에서 모델에 대한 입력은 sliding window {xt−τ,..,xt−1}\{x_{t-\tau}, .., x_{t-1}\}이며, 모델은 각 sliding window에 대해 boolean 값을 출력하여 해당 window 내에 anomaly가 있는지 여부를 예측함.

Overview

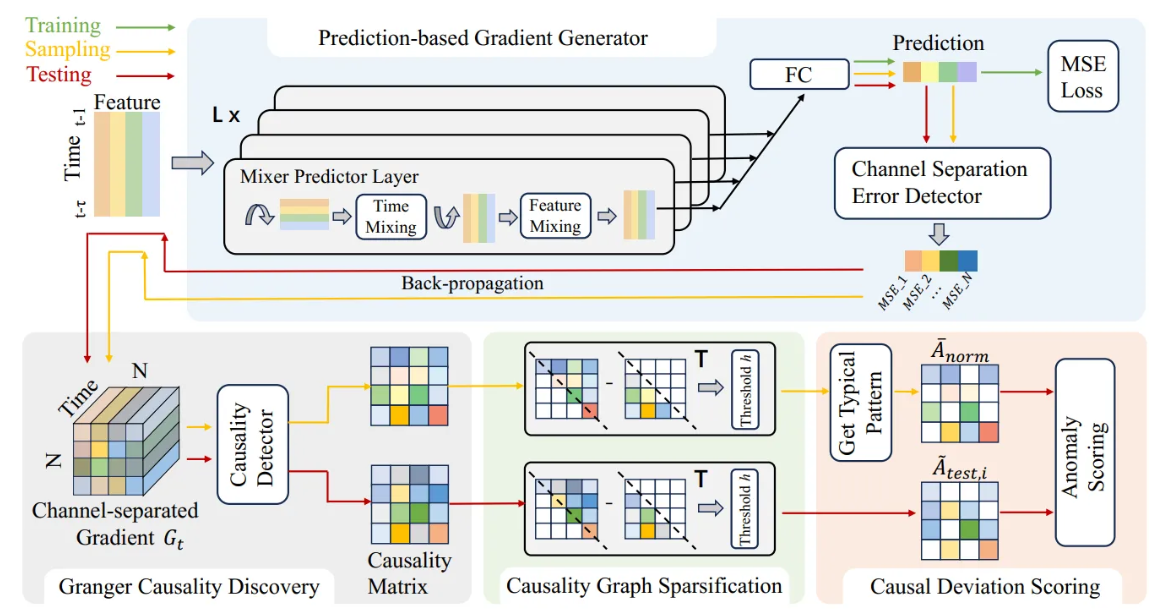
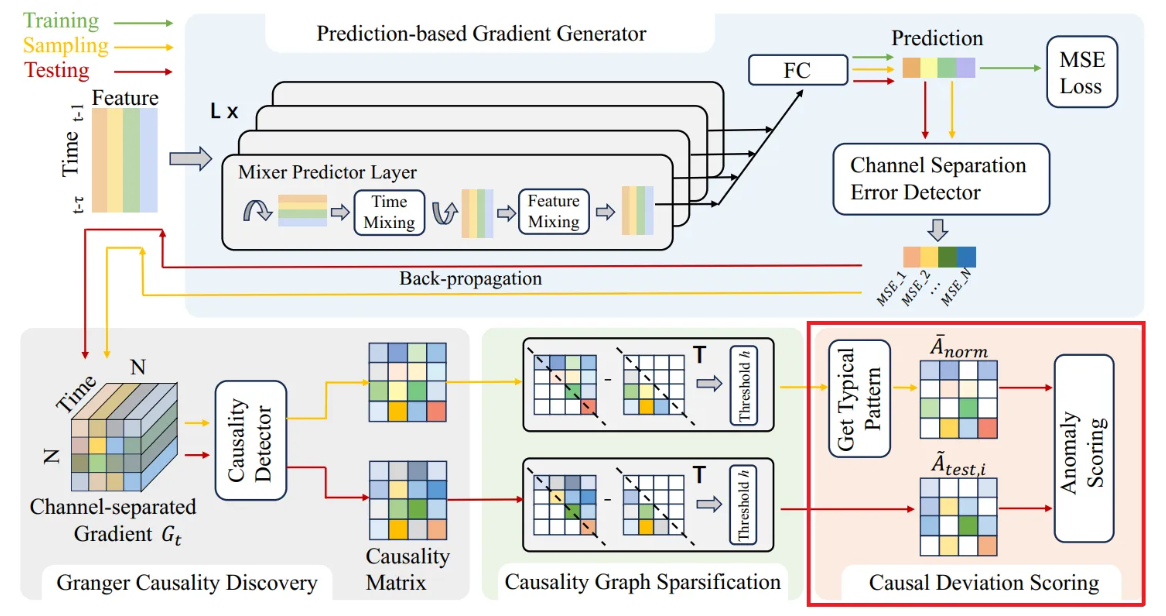
본 연구의 GCAD 프레임워크는 다변량 시계열 간의 Granger causality를 추출하고 test set의 causal pattern으로부터 anomaly를 식별하는 것을 목표로 함. 이는 주로 다음 네 파트로 구성됨.

  1. Prediction-based Gradient Generator
    • 예측 방법을 활용하여 학습을 안내하고 causality discovery 단계에서 channel-separated gradient를 제공
  2. Granger Casuality Discovery
    • Gradient generator에서 생성된 gradient로부터 Granger causal 관계를 동적으로 추론함
  3. Causality Graph Sparcification
    • 발견된 causal 관계에 sparsity 제약 조건을 적용하여 causality graph matrix를 얻음
  4. Causal Deviation Scoring
    • Causal pattern deviation score를 계산하고 시간 정보를 통합하여 이상을 탐지

Prediction-based Gradient Generator

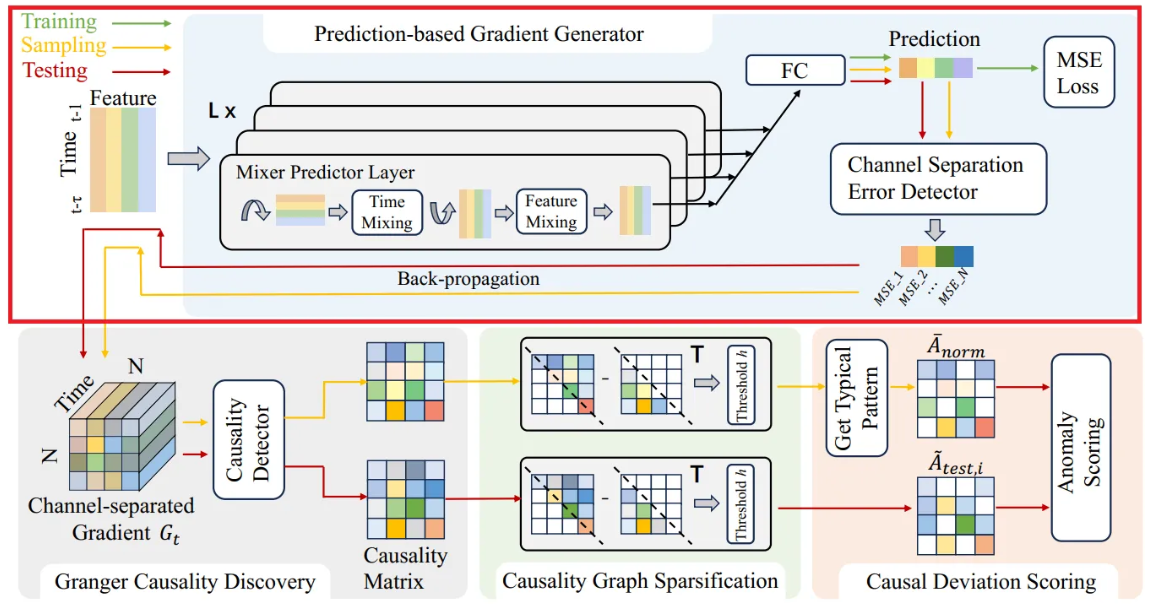
  • GCAD 프레임워크에서 시계열 데이터의 미래 값을 예측하는 모델 역할을 함
  • LL개의 stacked Mixer Predictor Layers로 구성되며, 각 layer는 interleaved temporal mixing 및 feature mixing MLP를 포함
    • Temporal mixing MLP는 모든 NN개의 feature에서 공유되는 반면, feature mixing MLP는 모든 time step에서 공유됨
    • 각 layer의 출력은 skip connection을 통해 fully connected layer로 공급되어 예측 출력을 생성
  • Predictor에 대한 입력은 sliding window Xt−1={xt−τ,xt−τ+1,...,xt−1}X_{t-1} = \{x_{t-\tau}, x_{t-\tau+1}, ..., x_{t-1}\}이며, 여기서 τ\tau는 Granger casuality에 대해 고려되는 최대 time lag이고 Xt∈RN×τX_t \in \mathbb R^{N \times \tau} 임.
  • Predictor의 출력은 시간 tt에 대한 예측 yt^=f(Xt−1)\hat {y_t} = f(X_{t-1})이고, 여기서 ff는 predictor에 의해 fitting 된 예측 함수이고, yt^∈RN\hat {y_t} \in \mathbb R^N임.
  • 학습 단계에서 predictor parameter의 최적화는 MSE loss를 사용
  • 테스트 단계에서 변수 간의 causal 관계를 탐색하기 위해 gradient generator는 변수 간의 pairwise predictor gradient를 계산해야하기 때문에, channel-separated Error detector를 제안하여 channel loss인 Lt,j=(y^t,j−yt,j)2L_{t, j} = (\hat y_{t, j} - y_{t, j})^2를 도입하였는데, 여기서 Lt,jL_{t, j}는 sliding window XtX_t에서 시퀀스 jj의 예측 오차를 나타냄.
  • 다음으로 gradient generator는 예측 네트워크를 통해 각 예측 오차에 대한 backpropagation을 수행하여 XtX_t에 대한 gradient Gt,j∈RN×τG_{t, j} \in \mathbb R^{N \times \tau}를 얻고, 모든 gradient를 compile하여 완전한 gradient tensor Gt∈RN×N×τG_t \in \mathbb R^{N \times N \times \tau} 를 구성함.

Granger Causality Discovery

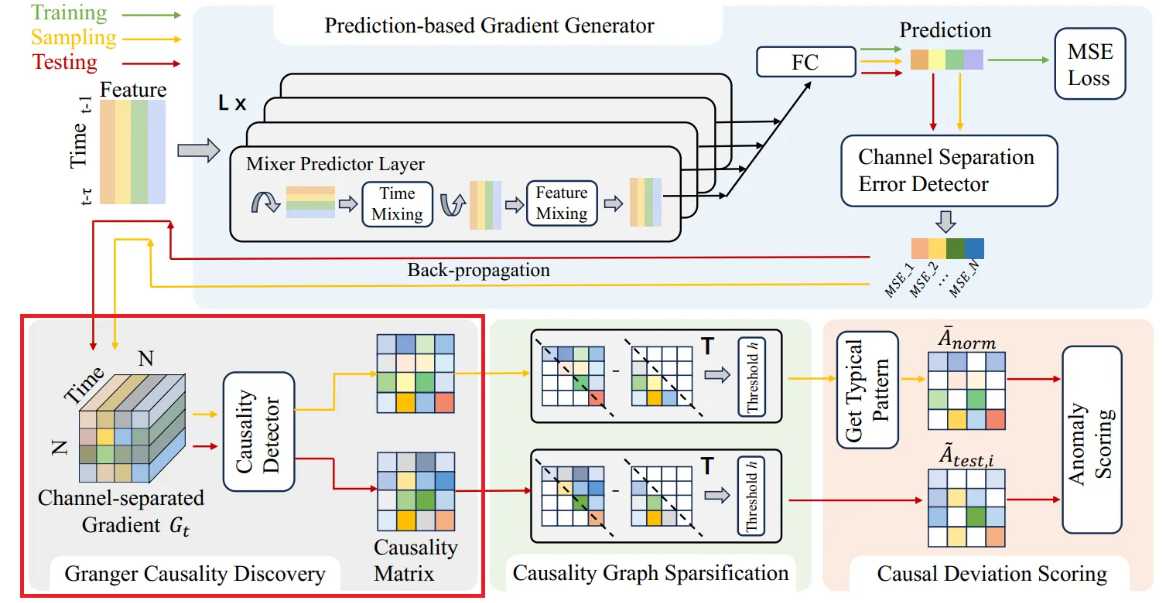
Nonlinear Granger causality는 변수가 서로의 예측 효과에 미치는 영향의 관점에서 정의됨


Definition 1

시계열 ii는 아래와 같은 경우에만 jj에 대해 Granger-cause 한다.

xt−τ:t−1,i′≠xt−τ:t−1,i,fj(xt−τ:t−1,1,...,xt−τ:t−1,i′,...,xt−τ:t−1,N)=fj(xt−τ:t−1,1,...,xt−τ:t−1,i,...,xt−τ:t−1,N)x'_{t-\tau : t-1, i} \not = x_{t-\tau:t-1, i}, \\ f_j(x_{t-\tau:t-1, 1} , ... , x'_{t-\tau:t-1, i} , ... , x_{t-\tau:t-1, N}) = f_j(x_{t-\tau:t-1, 1} , ... , x_{t-\tau:t-1, i} , ... , x_{t-\tau:t-1, N})

→ i.e., time series ii의 과거 데이터가 jj의 tt 시점의 데이터 예측에 영향을 미치는 경우


위 정의를 미분 관점에서 고려하면 t′∈(t−τ:t−1)t' \in (t - \tau : t-1)이고, xt′,i∗x^*_{t', i}를 Xt∈xt′,iX_t \in x_{t', i}의 perturbation이라고 할 때, xt′,i∗=xt′,i+Δx^*_{t', i} = x_{t', i} + \Delta이고, 여기서 Δ\Delta은 perturbation이다.


이전 하위 섹션에 설명된 예측 변수를 기반으로 아래 방정식을 얻을 수 있다.

y^t,j=fj(xt−τ:t−1,1,…,xt−τ:t−1,i,…,xt−τ:t−1,N),\hat y_{t,j} = f_j \left( x_{t-\tau:t-1, 1}, \ldots, x_{t-\tau:t-1, i}, \ldots, x_{t-\tau:t-1, N} \right),
y^t,j∗=fj(xt−τ:t−1,1,…,{xt−τ,i,,…,xt′,i∗,…,xt−1,i},…,xt−τ:t−1,N),\hat y^*_{t,j} = f_j \left( x_{t-\tau:t-1, 1}, \ldots, \{x_{t-\tau,i, }, \ldots, x^*_{t', i}, \ldots , x_{t-1, i}\} , \ldots , x_{t-\tau:t-1,N} \right),

여기서 fjf_j는 예측 네트워크에서 입력에 대한 y^t,j\hat y_{t,j}의 함수이다. perturbation으로 인해 발생한 예측 에러의 변화는 편미분 형태로 아래와 같이 변환될 수 있다:

lim⁡Δ→0∣Lt,j−Lt,j∗∣=∂Lt,j∂xt′,i⋅∣Δ∣\lim_{\Delta \to 0} \left| L_{t,j} - L^*_{t,j} \right| = \frac{\partial L_{t,j}}{\partial x_{t',i}} \cdot |\Delta|

여기서 Lt,j∗=(y^t,j∗−yt,j)2L^*_{t,j} = (\hat y^*_{t, j} - y_{t, j})^2이다. Granger causality는 최대 timelag 내에서 시퀀스 간 서로의 예측 값에 미치는 상호 영향을 고려한다. 따라서, 저자들은 Granger causality를 시간 지연 구간에 걸쳐 채널별로 분리된 기울기들의 절댓값을 적분한 값으로 정량화한다:

ai,j=∫t−τt−1∣∂Lt,j∂xϕ,i∣P(xϕ,i) dxϕ,ia_{i,j} = \int_{t-\tau}^{t-1} \left| \frac{\partial L_{t,j}}{\partial x_{\phi,i}} \right| P(x_{\phi,i}) \, dx_{\phi,i}

여기서 ϕ\phi는 t−τt-\tau에서 t−1t-1까지의 시간 인덱스이다. ai,ja_{i, j} 항은 관심분포 PP에 의해 파라미터화된 시퀀스 ii가 시퀀스 jj에 대해 얼마나 Granger cause를 일으키는지에 대한 정도이다.

Causality matrix는 A={ai,j}i,j=1NA = \{a_{i,j}\}^N_{i,j=1}로 정의된다.


Deep networks로 구성된 예측기는 역전파가 가능하므로, 예측 함수 ff는 본질적으로 연속적이고 미분 가능하다. 좀 더 단순화하기 위해, 관심 분포 PP는 uniform distribution으로 가정할 수 있다. 식 4에 따라, 만약 ai,j≠0a_{i,j} \not = 0이라면 두 예측 값이 같지 않다는 것을 의미하여, yˉt,j≠yt,j\bar y_{t, j} \not = y_{t, j}이다. 이 때, 두 예측 값에 대응하는 입력들이 각각 xt′,i∗x^*_{t', i}와 xt′,ix_{t',i}이므로, 시퀀스 ii의 입력이 다르면 시퀀스 jj의 출력도 달라진다. 이는 definition 1과 일치하며, 따라서 시퀀스 ii가 시퀀스 jj에 Granger causality를 갖는다고 할 수 있다.


Causality Graph Sparsification

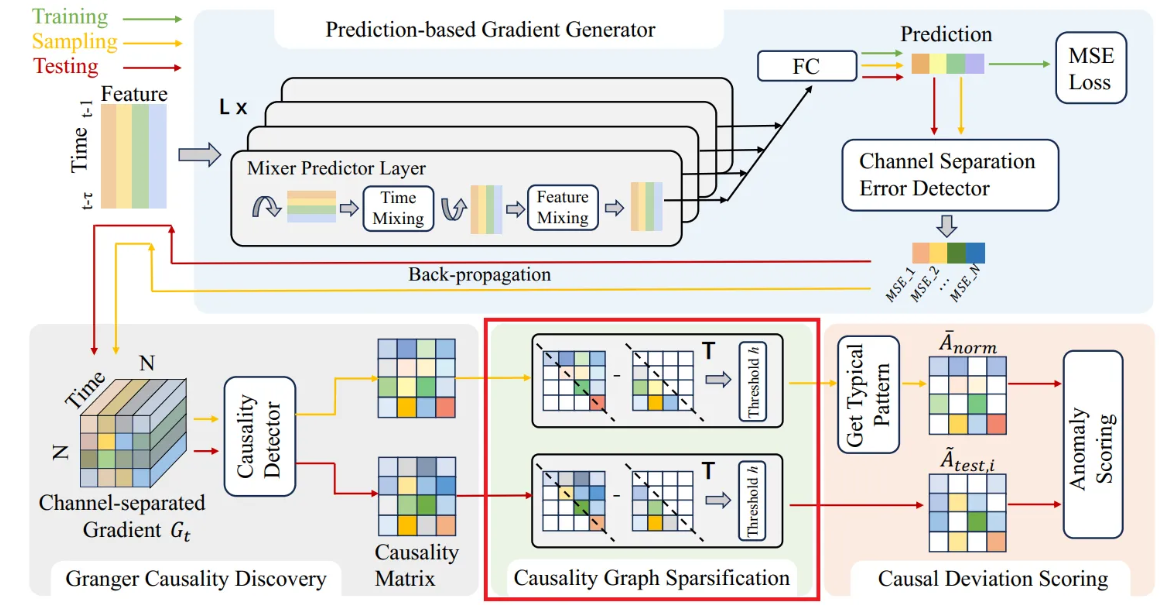
유사성이나 상관관계와 달리, 인과성은 반드시 단방향이어야 한다. 따라서 이상적인 Granger causality graph는 방향성이 있는 비순환 그래프(DAG) 형태이다. 하지만 nonlinear Granger causality 탐지에서는 인과성 그래프가 비순환적이라는 것을 엄격히 보장하기 어렵다.

기존 방법들은 희소성 제약을 통해 신경망 가중치에서 비선형 인과성을 발견하지만, 이상 탐지 작업에 적합하게 하기 위해서는 가중치를 직접 제약하는 대신 딥러닝 기울기에서 발견된 dynamic한 인과성을 희소화(sparsification)하는 방법을 사용한다.

이러한 희소화 과정은 미약하거나 유사성으로 나타나는 양방향 연결을 제거하고, 강한 단방향 인과관계만 남기는 방식으로, 수학적으로는 아래와 같이 표현된다:

A^i,j=max(0,Ai,j−Aj,i),i≠j\hat A_{i, j} = max(0, A_{i,j} - A_{j, i}), i \not = j
A^i,i=Ai,i\hat A_{i,i} = A_{i,i}

여기서 AA는 casaulity 행렬이며, A^\hat A는 희소화 된 causality graph 행렬이다. 이 연산은 양방향 연결에서 대칭적 유사성을 제거하여 단방향 인과성을 강조한다.

추가적으로, 임계값 hh를 설정하여 특정 값 이하의 인과 효과를 0으로 만들어, 노이즈를 줄이고 causality graph를 더 정제한다.


Causal Deviation Scoring

먼저 정상 상태 데이터를 여러 개의 윈도우 샘플로 무작위 추출한 후, 이 샘플들을 WtrainW_{train}이라고 하고, 베르누이 분포로 샘플링하여 Wtrain′W'_{train}을 만든다.

각 샘플에 대해 causality graph를 계산하는 함수 g(⋅)g(·)를 사용해서 nn개의 causality graph를 구한다:

Anorm,i=g(Wtrain,i′),   i=1,2,...,nA_{norm, i} = g(W'_{train, i}), \ \ \ i = 1,2,...,n

이 causality matrix는 희소화 과정을 거친 행렬 A^norm,i\hat A_{norm ,i}가 되고, 그 평균을 구해 normal causality pattern AnormA_{norm}으로 정의한다:

Anorm=1n∑i=1nA^norm,iA_{norm} = \frac 1 n \sum^n_{i=1}\hat A_{norm, i}

테스트 데이터도 같은 방식으로 슬라이딩 윈도우를 적용하여 윈도우별 인과성 그래프를 만든다:

A^test={g(Wtest,i)}i=1m\hat A_{test} = \{g(W_{test, i})\}^m_{i=1}

여기서 mm은 테스트 윈도우 개수이다.


각 테스트 causality graph와 정상 normal causality pattern 간 절대 편차를 정규화하여 다음과 같이 score로 만든다:

Sc,i=∑∣A^test,i−Anorm∣∑∣Anorm∣+ϵS_{c, i} = \frac {\sum |\hat A_{test, i} - A_{norm}|}{\sum |A_{norm}| + \epsilon}

여기서 분자는 두 그래프의 원소별 차이의 절댓값의 합이고, 분모는 normal causality pattern 행렬 원소의 절댓값 합으로 정규화하는 역할을 한다.


Causality pattern 행렬의 대각 원소는 각 변수 자신의 시간 의존성을 대변한다. 아래와 같이 대각 원소들만 뽑아서 정상과 테스트 간 차이를 계산한다:

St,i=∑∣diag(A^test,i)−diag(Anorm)∣∑∣diag(Anorm∣+ϵS_{t, i} = \frac {\sum |diag(\hat A_{test, i}) - diag(A_{norm})|}{\sum |diag(A_{norm}| + \epsilon}

이렇게 얻은 인과성 편차 점수 ScS_c와 시간 패턴 편차 점수 StS_t를 결합하여 아래와 같은 최종 점수를 만든다:

Si=Sc,i+β⋅St,iS_i = S_{c, i} + \beta · S_{t, i}

Experimental Results

Anomaly Detection Performance

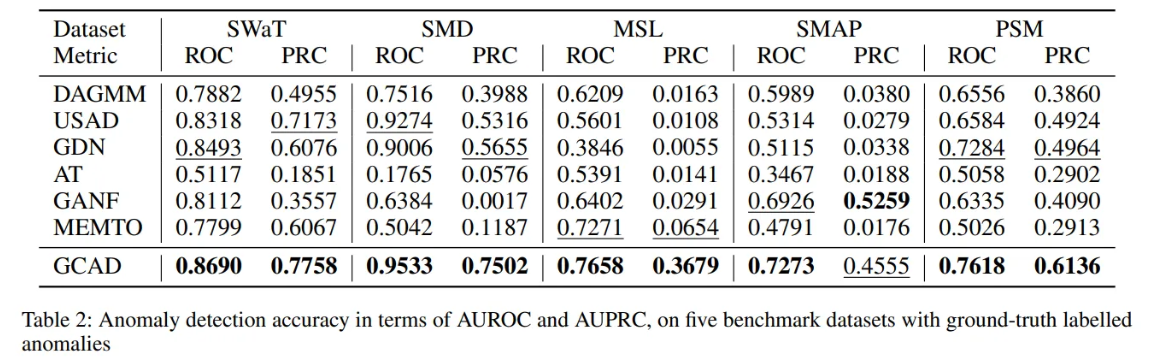
  • Baseline 모델들과 5가지 real-world 데이터셋들에서 비교 실험을 수행한 결과, GCAD는 다변량 시계열 이상 탐지에서 대부분의 벤치마크 데이터셋에서 SOTA 성능을 달성하였다.
  • DAGMM과 USAD 같은 기존 방법들은 변수 간 공간적 관계를 명시적으로 모델링하지 않아 이상 탐지 성능이 낮은 편이다.
  • GDN은 적응형 그래프 구조 학습을 이용하지만, 고정된 그래프 구조 학습으로 동적 변화에 취약할 수 있다.
  • GANF는 분포 변화가 심각한 데이터셋인 SMAP에서는 우수한 성능을 보이나, 전체적으로 GCAD가 더 일관된 성능 개선을 보인다.

Ablation Study

제안된 프레임워크 GCAD의 각 구성 요소가 성능에 미치는 영향을 평가하였다.

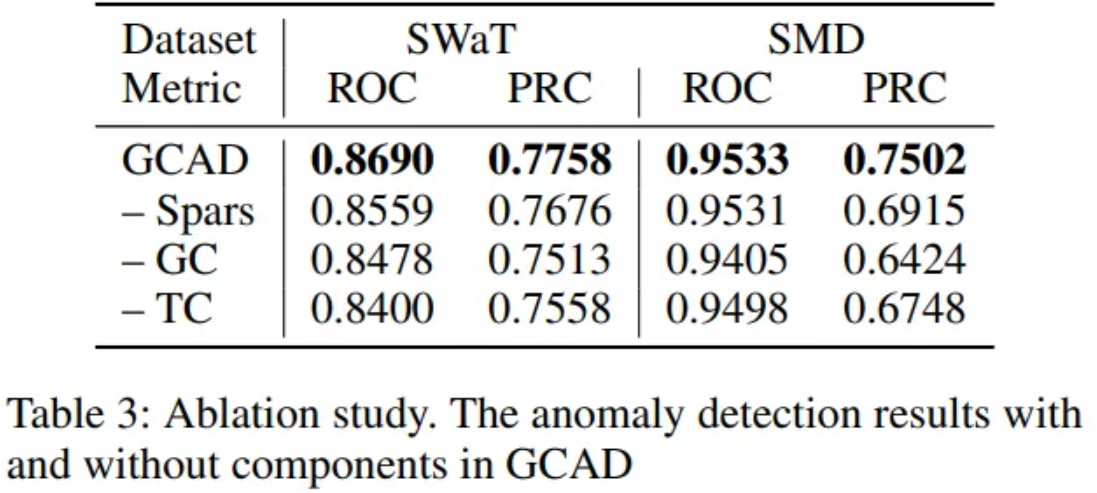
Table 3 결과에 따르면, Causality Graph 희소화 작업 제거 시 성능이 감소하는데, 이는 희소화가 유사성으로 인해 탐지되는 인과 관계의 노이즈를 줄이는 데 도움을 주었기 때문이라고 한다.

또한, Granger causality를 활용하지 않거나(-GC), 시간적 패턴 편차를 무시할 경우(-TC)도 성능이 하락하여, 인과 관계와 시간 정보를 모두 통합하는 것이 이상 탐지의 정확도를 높인다는 점을 보여준다.


Effect of Parameters

GCAD의 이상 탐지 성능에 대한 주요 하이퍼파라미터의 영향을 추가로 실험하였다. 모든 실험은 SWaT 데이터를 사용하여 수행되었다.

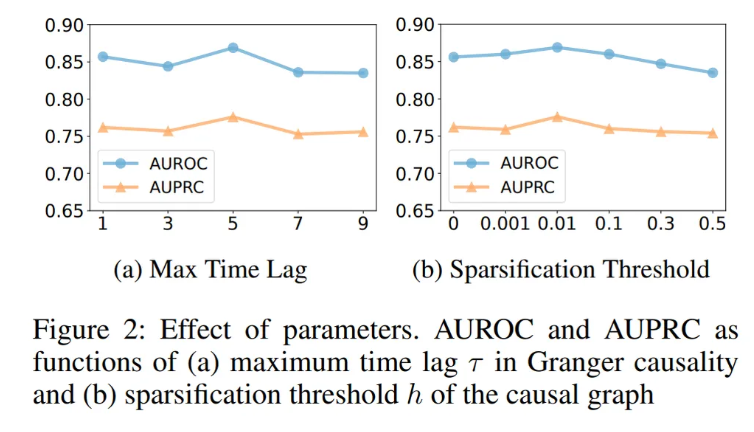
  • Max time lag τ\tau는 Granger causality를 발견할 때 고려하는 과거 시점의 최대 간격을 의미한다.
    • τ\tau가 1일 경우, 한 시점 전만 고려하여 인과성을 확인하므로 단기적이고 인접한 시간 간격에서 발생하는 이상 탐지에 민감하다.
    • τ\tau값이 커질수록 보다 복잡하고 고차원적인 시공간 패턴을 포착할 수 있으나, 단기 이상 민감도는 떨어질 수 있다.
    • 적당한 τ\tau값은 복잡한 이상 징후 탐지와 단기 이상 민감도 간 균형을 맞출 수 있다.
  • Sparsification threshold hh는 causality graph에서 노이즈로 간주되는 작지만 의미없는 인과 관계를 제거하는 기준이 된다.
    • hh가 너무 작으면 non-zero지만 의미없는 인과성이 많이 남아 이상 탐지에 방해가 된다.
    • hh가 너무 크면 중요한 원인관계도 제거되어 시스템 내 정보 활용도가 떨어진다.
    • 따라서 적당한 hh값을 선정하여 균형을 맞추어줘야 한다.

Analysis of Anomaly Detection Examples

Causality pattern이 어떻게 이상을 드러내는지를 보여주기위해 실제 시스템의 이상 이벤트 데이터에 대한 case study를 수행하였다. 마찬가지로 SWaT 데이터에서 수행되었다. SWat 시스템은 수처리 공정으로, 복잡한 물리적 관계를 가진 센서들이 여러 단계에 위치해 있다.

  • 이상 이벤트 발생 시점에서 GCAD가 계산한 causality pattern matrix를 시각화한 그림
  • 행렬의 각 원소는 해당 시점에서의 causality 강도가 정상 상태 패턴과 얼마나 차이나는지를 나타냄
  • 색이 짙을수록 정상과 큰 차이가 있는 변수 쌍을 의미하며, 이는 이상 상황에서 변수 간 인과 관계가 변화했음을 보여줌
  • 위 행렬을 통해 특정 펌프 공격이 downstream의 여러 센서에 미치는 영향을 직관적으로 파악할 수 있다.

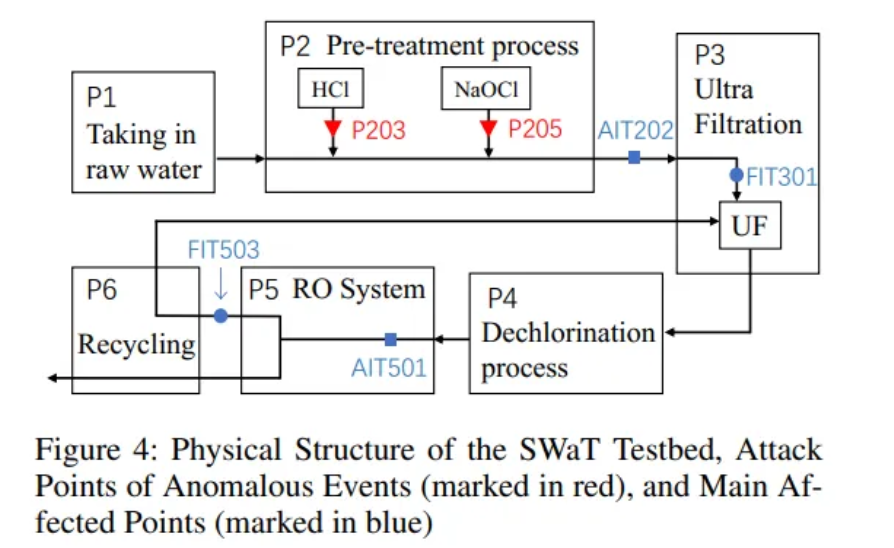
구체적으로 SWaT 테스트베드의 구조를 보았을 때, 이상 공격 지점(P203, P205)으로 인해 영향을 받는 주요 센서는 AIT202, AIT501, FIT301, FIT503임을 확인할 수 있는데, 그림 3의 causality pattern에서 두드러지는 센서들이 물리적으로도 공격 지점과 연관되어있음을 보여준다. 이는 GCAD가 단순한 통계적 수치 이상의 의미있는 인과 경로를 포착하고 있다는 중요한 근거가 된다.


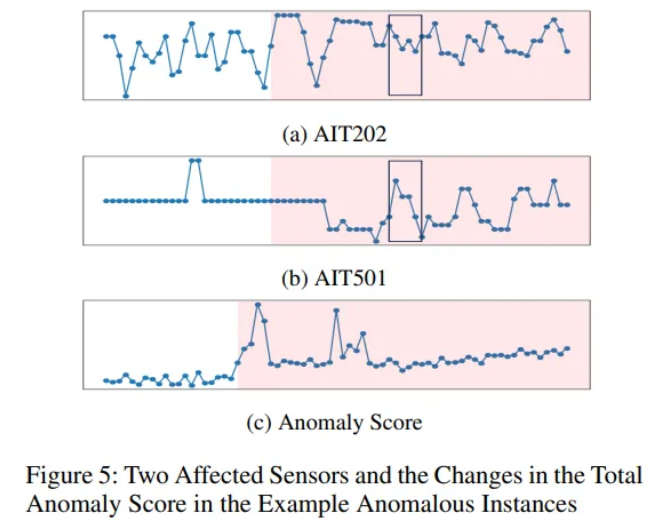
  • (a), (b)에서는 이상 공격 시점에서 센서 AIT202와 AIT501의 시계열 데이터 변화를 보여주는데, 육안으로는 큰 변화를 관찰하기 어렵다.
  • (c)에서는 GCAD가 계산한 이상 점수가 시간에 따라 어떻게 변화하는지 나타내는데, 이상 공격 구간(빨간색 표시)에서 이상 점수가 크게 상승하는 것을 볼 수 있다.
    • 즉, GCAD는 개별 시계열 단독 관찰로는 파악하기 어려운 미묘한 이상도 causality pattern 변화를 통해 효과적으로 탐지함을 보여준다.
profile
shyoon
큰 사람이 되겠어요
이전 포스트

InvAgent: A Large Language Model based Multi-Agent System for Inventory Management in Supply Chains

다음 포스트

[논문 리뷰] Root Cause Analysis of Anomalies in Multivariate Time Series Through Granger Causal Discovery (ICLR 2025)

0개의 댓글