딥러닝의 학습 과정을 모르는 건 아니지만... 한 번쯤은 정리해 두는 것이 좋을 것 같아서 기록을 남긴다 !

---

딥러닝 학습 과정

 딥러닝의 학습 과정은 "Forward Propagation -> Loss 계산 -> Backward Propagation -> 파라미터 갱신"의 반복으로 이루어진다. 이러한 반복을 통해 Loss를 최소화하는 최적의 파라미터를 찾는 것이 딥러닝을 통한 학습이다.

 각각의 단계에 대해 한 번 살펴보자.

Forward Propagation

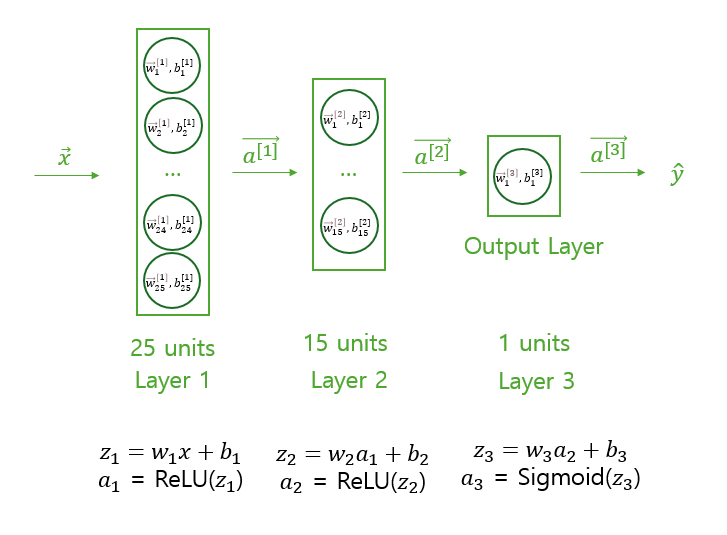
 Binary Classification을 위한 간단한 신경망을 구성한다고 가정했을 때, Forward Propagation은 입력 데이터에 대해 각 층에서 가중치(𝑊)와 편향(𝑏)을 적용한 선형 변환 (𝑊𝑥+𝑏)을 수행한 후, 활성화 함수를 거쳐 비선형성을 추가하는 과정이다. 이 과정에서 각 층의 출력값이 다음 층의 입력값이 되며, 최종적으로 출력층에서 예측값을 계산하게 된다. 이 과정을 신경망의 모든 층에서 반복하는 것이 Forward Propagation이다.

이때, 출력층에서 Sigmoid를 사용하는 이유는 Binary Classification의 출력은 0 또는 1인데, Sigmoid를 사용하면 출력이 0~1 사이이기 때문에 이를 확률적으로 계산해 손실 함수 계산을 더 용이하게 하기 때문이다.

Loss 계산

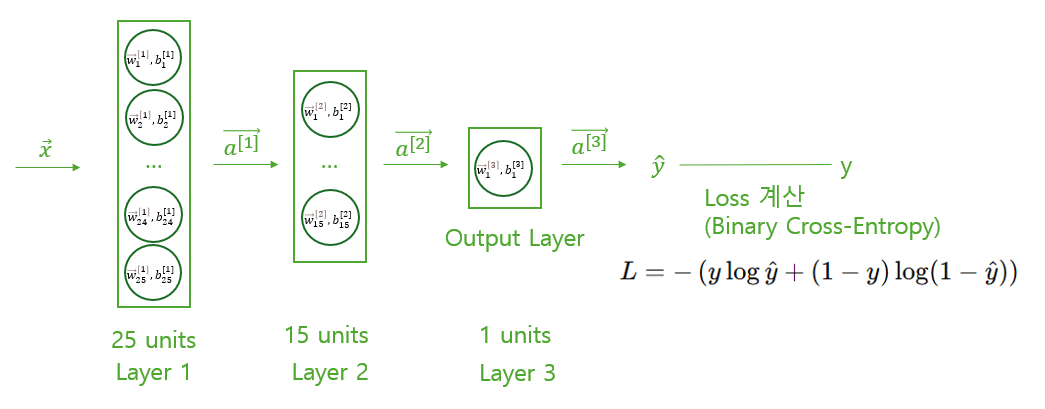
 다음으로, Forward Propagation의 결과로 출력된 확률적인 값을 통해 정답과 예측값 사이의 오차를 계산해 준다.

Backward Propagation

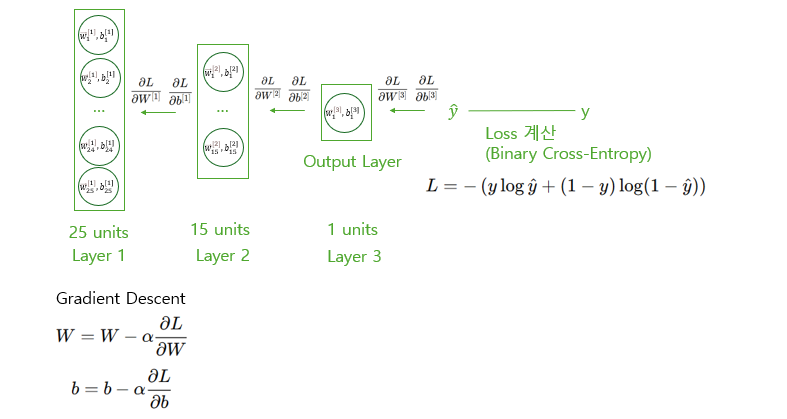
 Backward Propagation은 손실 함수와 파라미터 간의 기울기 변화량을 구하고, 이를 통해 가중치와 편향을 갱신해 나가는 과정을 의미한다.

 파라미터 갱신은 Gradient Descent, Adam, RMSprop 등의 옵티마이저를 사용할 수 있으나, 여기서는 Gradient Descent를 활용했다.

 그림으로 보면 다음과 같다. Loss Function의 결과와 파라미터 W, b의 기울기 변화량을 구하고, Gradient Descent 식을 통해 파라미터를 동시에 갱신하는 것을 그림을 통해 확인할 수 있으며, 이때 파라미터의 갱신 반드시 "동시에" 일어나야 한다.

 이때, 파라미터 갱신을 위한 미분값을 바로 구하기 어렵기 때문에 Chain Rule을 통해 기울기를 계산한다.

 Chain Rule은 어떤 함수가 여러 개의 함수로 구성되어 있을 때, 각 부분 함수의 미분을 곱하여 전체 미분을 계산하는 방식을 의미한다.
(ex) y가 u의 함수이고, u가 x의 함수일 때, (y = f(u), u = g(x))

 이렇게 Chain Rule을 통해 기울기를 계산하고, 계산된 기울기를 바탕으로 옵티마이저를 활용해 파라미터를 갱신하는 일련의 과정을 Backward Propagation이라고 하며, 딥러닝에선 각 에폭마다 Forward Propagation -> Loss 계산 -> Backward Propagation의 과정을 반복하고, 여러 에폭을 거쳐 최적의 파라미터를 찾아간다. 이것이 딥러닝이 학습하는 방식이다.