
3과목 - 데이터분석
1. R기초와 데이터 마트
R기초 (최근 잘 안나옴)
데이터 전처리
-데이터를 분석하기 위해 데이터를 가공하는 작업
(1) 요약변수: 수집된 정보를 종합한 변수로서 재활용성이 높음 (1개월간 수입)
(2) 파생변수: 의미를 부여한 변수, 논리적 타당성 필요 (고객구매등급)
R에서의 데이터 전처리 패키지
(1)reshape: melt로 녹인 데이터를 cast로 재구조화
(2)sqldf: R에서 SQL을 활용하여 데이터프레임(DF)을 다룰 수 있게 해줌
(3)plyt: apply 함수 기반 데이터 처리
(4)data.table: 컬럼별 인덱스로 빠른 처리가 가능한 데이터 구조
데이터 마트
데이터 마트(DM)
-데이터 웨어 하우스의 한 분야로 특정 목적을 위해 사용 (소규모 데이터웨어하우스)
결측값과 이상값 검색
EDA(탐색적 자료 분석)
-데이터의 의미를 찾기 위해 통계, 시각화를 통해 파악
-EDA의 4가지 주제: 저항성의 강조, 잔차 계산, 자료변수의 재표현, 그래프를 통한 현시성
-> '저잔재현'
결측값
-존재하지 않는 데이터 null/NA로 표시, 의미 있는 데이터 일수도 있음
(1)단순 대치법
-결측값 가지는 데이터를 삭제
-complete.cases 함수가 FALSE면 데이터에 결측값 제거 (TRUE면 제거하면 안됨)
(2)평균 대치법
-평균으로 대치
(3)단순 확률 대치법
-가까운 값으로 변경(KNN을 활용)
(4)다중 대치법
-여러 번 대치(대치 -> 분석 -> 결합)
이상값
-극단적으로 크거나 작은 값이며, 의미 있는 데이터 일수도 있음(ex. 체중 3kg)
-이상값을 항상 제거하는 것은 아님
(1)ESD(Extreme Studentized Deviation)
-평균으로부터 표준편차의 3배가 넘어가는 데이터는 이상값으로 판단
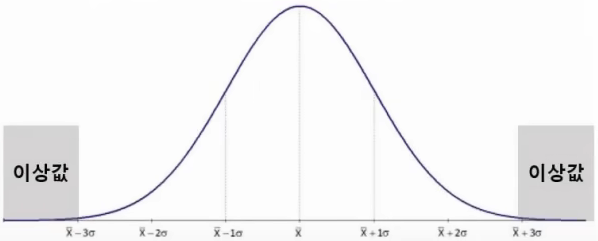
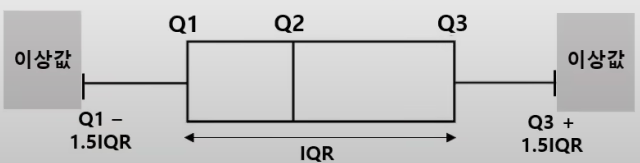
(2)사분위수
-Q1 -1.5IQR보다 작거나, Q3 + 1.5IQR보다 크면 이상값으로 판단
2. 통계분석
통계학 개론
전수조사와 표본조사
-전수조사: 전체를 다 조사, 시간과 비용 많이 소모
-표본조사: 일부만 추출하여 모집단을 분석
표본 추출 방법 (집략 추출과 층화 추출의 차이를 명확하게 구분하자)
(1)랜덤 추출법: 무작위로 표본 추출
(2)계통 추출법: 번호 부여하여 일정 간격으로 추출
(3)집략 추출법
-여러 군집으로 나눈 뒤 군집을 선택하여 랜덤 추출
-군집 내 이질적 특징, 군집 간 동질적 특징
(4)층화 추출법
-군집 내 동질적 특징, 군집 간 이질적 특징
-같은 비율로 추출 시, 비례 층화 추출법
(5)복원, 비복원 추출
-복원 추출: 추출되었던 데이터를 다시 포함시켜 표본 추출
-비복원 추출: 추출되었던 데이터는 제외하고 표본 추출
자료의 척도 구분
(1)질적 척도
-명목척도: 어느 집단에 속하는지 나타내는 자료(대학교, 성별)
-순서척도(서열척도): 서열관계가 존재하는 자료(학년, 순위)
(2)양적 척도
-등간척도(구간척도): 구간 사이 간격이 의미가 있으며 덧셈과 뺄셈만 가능(온도, 지수 등)
-비율척도: 절대적 기준 0이 존재하고 사칙연산 가능한 자료(무게, 나이 등)
기초 통계량
(1)평균(기댓값): 전체 합을 개수로 나눈 값
(2)중앙값: 자료를 크기 순으로 나열했을 때 가운데 값
(3)최빈값: 가장 빈번하게 등장하는 값
(4)분산: 자료들이 퍼져있는 정도 / 표준편차: 분산의 제곱근 값
(5)공분산: 두 확률변수의 상관정도
-공분산 = 0: 상관이 전혀 없는 상태
-공분산 > 0: 양의 상관관계 (+inf 까지)
-공분산 < 0: 음의 상관관계 (-inf 까지)
-최소, 최대값이 없어 강약 판단 불가
(6)상관계수
-상관정도를 -1 ~ 1값으로 표현
-상관계수 = 1: 정비례 관계
-상관계수 = -1: 반비례 관계
첨도와 왜도
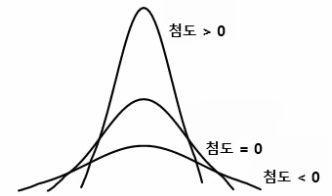
(1)첨도: 자료의 분포가 얼마나 뾰족한 지 나타내는 척도
-첨도 = 0: 정규 분포 형태
-> 3을 기준으로 정규분포 형태를 판단하기도 함
-값이 클수록 뾰족한 모양
(2)왜도: 자료 분포의 비대칭 정도(0일 때 대칭)
-왜도 < 0: 최빈값 > 중앙값 > 평균값
-왜도 > 0: 최빈값 < 중앙값 < 평균값
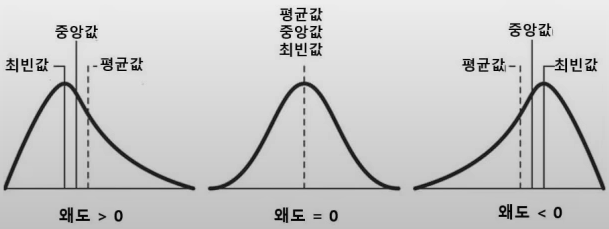
-> 평균값은 꼬리를 따라감
Summary함수 결과의 해석

수치형 변수는 회귀 분석, 범주형 변수는 분류분석
기초 확률 이론
(1)조건부 확률: 특정 사건 B가 발생했을 때 A가 발생할 확률
-P(A|B) = P(A∩B)/P(B) (백신을 맞았을 때 감기에 걸릴 확률)
(2)독립사건: A, B가 서로 영향을 주지 않는 사건(P(A|B) = P(A))
-P(A∩B)=P(A)P(B) (주사위 A가 3이 나왔을 때, 주사위 B가 3이 나올 확률)
(3)배반사건: A, B가 서로 동시에 일어나지 않는 사건
-P(A∩B)=∅ (동전을 던졌을 때 앞면과 뒷면이 동시에 나올 확률)
확률분포
-확률변수가 특정한 값을 가질 확률을 나타내는 함수
(1)이산 확률분포
-값을 셀 수 있는 분포, 확률질량함수로 표현
1)이산균등분포: 모든 곳에서 값이 일정한 분포
2)베르누이분포: 매 시행마다 오직 두 가지의 결과 뿐인 분포
3)이항분포: n번의 독립적인 베르누이 시행을 통해 성공할 확률 p를 가지는 분포
4)기하분포: 처음 성공이 나올 때까지 시도횟수를 확률변수로 가지는 분포
5)다항분포: 여러 개의 값을 가질 수 있는 확률 변수들에 대한 분포
6)포아송분포: 단위 공간 내에서 발생할 수 있는 사건의 발생 횟수를 표현하는 분포
->'베포항항하'
(2)연속 확률분포
-값을 셀 수 없는 분포, 확률밀도함수로 표현
1)정규분포: 우리가 일상생활에서 흔히 보는 가우스분포(Z검정)
2)t분포: 두 집단의 평균치 차이의 비교 검정 시 사용(T검정)
-데이터 개수가 30개 이상이면 정규성 검정 불필요
3)카이제곱분포: 두 집단의 동질성 검정, 혹은 단일 집단 모분산에 대한 검정(카이제곱 검정)
4)F분포: 두 집단의 분산의 동일성 검정 시 사용(F검정)
(3)확률변수 X의 f(x) 확률분포의 대한 기댓값(E(X))
1)이산적 확률변수: E(X) = ∑xf(x)
2)연속적 확률변수: E(X) = ∫xf(x)
추정
-표본으로부터 모집단을 추측하는 방법
(1)점추정: 모집단이 특정한 값
(2)구간추정: 모집단이 특정한 구간(95%, 99%를 가장 많이 사용)
가설검정(매우 중요)
-모집단의 특성에 대한 주장을 가설로 세우고 표본조사로 가설의 채택여부를 판정
(1)귀무가설(H0): 일반적으로 생각하는 가설(차이가 없다)
(2)대립가설(H1): 귀무가설을 기각하는 가설, 증명하고자 하는 가설(차이가 있다, 크다/작다)
(3)유의수준(α): 귀무가설이 참일 때 기각하는 1종 오류를 범할 확률의 허용 한계(일반적 0.05 = 5%)
(4)유의확률(p-value): 귀무가설을 지지하는 정도를 나타내는 확률

가설 검정 문제 풀이 방법(1번부터 5번까지 순서대로)
1)귀무가설 / 대립가설 설정
-'차이가 없다'혹은 '동일하다' -> 귀무가설
2)양측 혹은 단측검정 확인
-대립가설의 값이 '같지 않다' -> 양측검정 / '값이 크다', '값이 작다' -> 단측검정
3)일표본 혹은 이표본 확인
-하나의 모집단 -> 일표본 / 두개의 모집단 -> 이표본
4)귀무가설 기각 혹은 채택
-p-value < 유의수준(α) -> 귀무가설 기각 / p-value > 유의수준(α) -> 귀무가설 채택
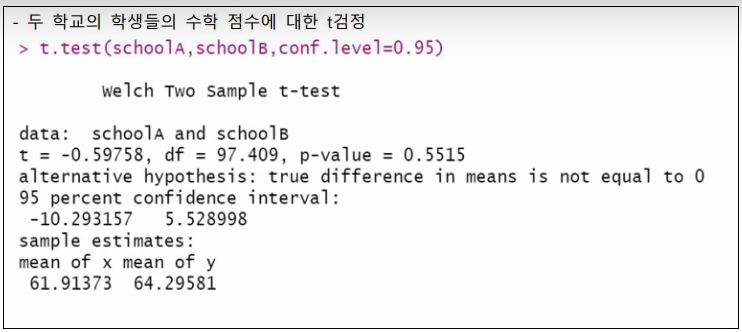
5)t검정인 경우 - 단일표본, 대응표본, 독립표본 확인
-모집단에 대한 평균검정 -> 단일표본
-동일 모집단에 대한 평균비교 검정 -> 대응표본
-서로 다른 모집단에 대한 평균비교 검정 -> 독립표본

비모수검정
(1)모집단에 대한 아무런 정보가 없을 때
(2)관측 자료가 특정 분포를 따른다고 가정이 불가할 때
(3)부호검정, 순위합검정, 만-휘트니 U검정, 크러스컬-월리스 검정
기초 통계 분석
회귀분석
(1)개념: 독립변수들이 종속변수에 미치는 영향을 파악하는 분석방법
1)독립변수: 원인을 나타내는 변수 (x)
2)종속변수: 결과를 나타내는 변수 (y)
3)잔차: 계산값과 예측값의 차이(오차: 모집단 기준, 잔차: 표본집단 기준)
(2)회귀계수 추정방법
-최소제곱법: 잔차의 제곱합이 최소가 되는 회귀계수와 절편을 구하는 방법 (중요)
(3)회귀모형 평가
-R-squared: 총 변동 중에서 회귀모형에 의하여 설명되는 변동이 차지하는 비율 (0 ~ 1)
회귀분석의 가정(자주 나옴)
(1)선형성: 종속변수와 독립변수는 선형관계
(2)등분산성: 잔차의 분산이 고르게 분포
(3)정상성(정규성): 잔차가 정규분포의 특성을 지님
(4)독립성: 독립변수들 간 상관관계가 없음
-정규성은 Q-Q plot, 샤피로 윌크 검정, 히스토그램, 왜도와 첨도 활용 확인
회귀분석 종류
(1)단순회귀: 1개의 독립변수와 종속변수의 선형관계
(2)다중회귀: 2개 이상의 독립변수와 종속변수의 선형관계
(3)다항회귀: 2개 이상의 독립변수와 종속변수가 2차 함수 이상의 관계
(4)릿지회귀: L2 규제를 포함하는 회귀 모형
(5)라쏘회귀: L1 규제를 포함하는 회귀 모형
(규제는 일반화를 위해)
회귀분석의 분산분석(ANOVA)표
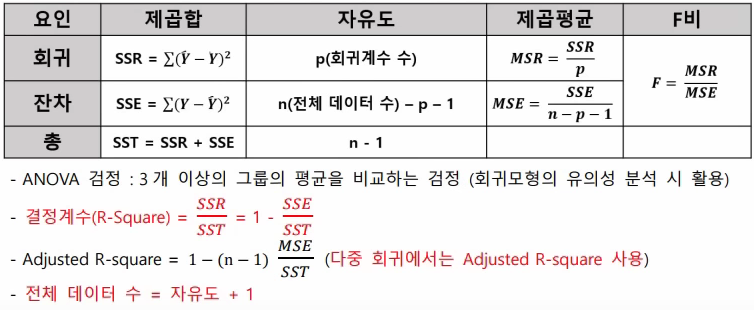
(제곱합, 자유도 값을 주고 제곱평균, F비 계산하는 식으로 나옴)
회귀 모형의 검정(순서대로)
1)독립변수와 종속변수 설정
2)회귀계수 값의 추정
3)모형이 통계적으로 유의미한가: 모형에 대한 F 통계량, p-value
-귀무가설: '모든 회귀계수는 0이다'
4)회귀계수들이 유의미한가: 회귀계수들의 t 통계량, p-value
-각각의 회귀계수에 대한 귀무가설: '회귀 계수는 0이다'
5)위 1), 2) 모두를 기각하면 해당 모델을 활용
6)모형이 설명력을 갖는가: 결정계수(R square) 값

(신뢰도가 주어져있지 않으면 95%라고 생각하고 풀면 됨)
(DF: Degree of Freedom, 자유도)
(Intercept: 절편)
최적의 회귀 방정식 탐색 방법
(1)전진선택법: 변수를 하나씩 추가하면서 최적의 회귀방정식을 찾아내는 방법
(2)후진제거법: 변수를 하나씩 제거하면서 최적의 회귀방정식을 찾아내는 방법
(3)단계별 선택법: 전진선택법 + 후진선택법으로 변수를 추가할 때 벌점을 고려
1)AIC(아카이케 정보 기준)
-편향과 분산이 최적화되는 지점 탐색, 자료가 많을수록 부정확
2)BIC(베이즈 정보 기준)
-AIC를 보완했지만 AIC보다 큰 패널티를 가지는 단점, 변수가 적은 모델에 적합
다변량 분석
상관분석
-두 변수간의 선형적 관계가 존재하는지 파악하는 분석
(1)종류
1)피어슨 상관분석: 양적 척도, 연속형 변수, 선형관계 크기 측정
2)스피어만 상관분석: 서열 척도, 순서형 변수, 선형/비선형적 관계 나타냄
(2)다중공선성
-다중회귀분석에서 설명변수들 사이에 상관관계가 클 때 모델을 불안정하게 만듦
다차원 척도법(MDS: MultiDimensional Scaling)
-데이터 간의 근접성을 시각화(2차원 평면이나 3차원 공간에 표현)
(1)특징: 데이터 축소 목적, Stress 값이 0에 가까울 수록 좋음, x/y축 해석이 불가
(2)종류
1)계량적 MDS: 양적척도 활용
2)비계량적 MDS: 순서척도 활용
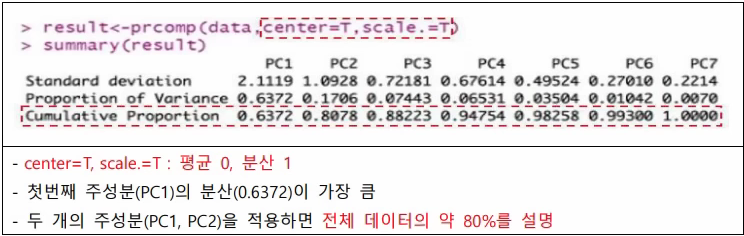
주성분 분석(PCA)
-상관성 높은 변수들의 선형 결합으로 차원을 축소하여 새로운 변수를 생성
-자료의 분산이 가장 큰 축이 첫 번째 주성분
-70 ~ 90%의 설명력을 갖는 수를 결정
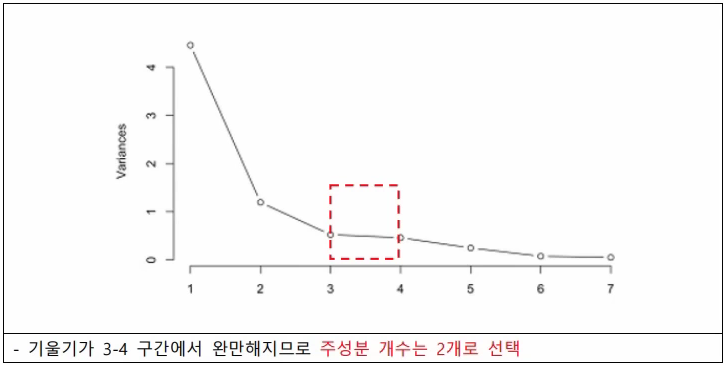
(1)스크리플롯(Screeplot)
-주성분의 개수를 선택하는데 도움이 되는 그래프(x축은 주성분 개수, y축은 분산변화)
-수평을 이루기 바로 전 단계 개수로 선택
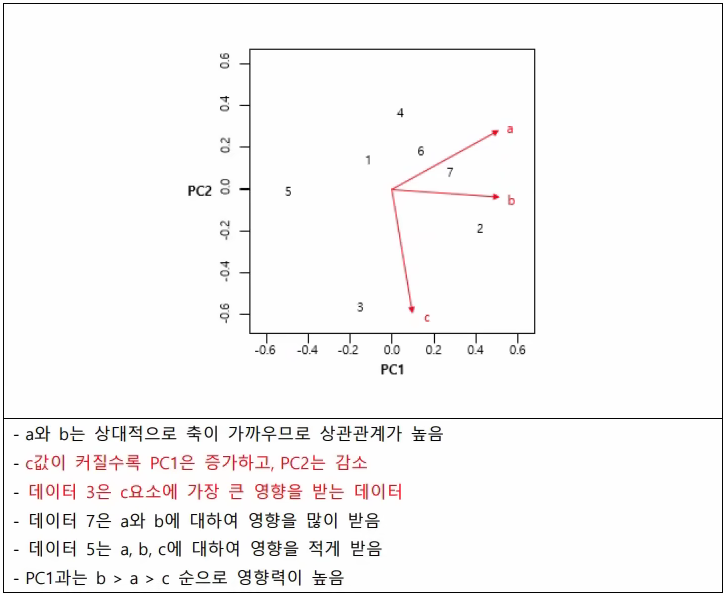
(2)바이플롯
-데이터간 유사도를 한번에 볼 수 있는 그래프(x축은 첫번째 주성분, y축은 두번째 주성분)
-PC와 평행할수록 해당 PC에 큰 영향
-화살표의 길이가 길수록 분산이 큼
시계열 예측
시계열 분석
-시간의 흐름에 따라 관찰된 자료의 특성을 파악하여 미래를 예측(주가데이터, 기온데이터)
정상성
-시계열 예측을 위해서는 모든 시점에 일정한 평균과 분산을 가지는 정상성을 만족해야 함
-정상시계열로 변환 방법
1)차분: 현 시점의 자료를 이전 값으로 빼는 방법
2)지수변환, 로그변환
백색 잡음
-시계열 모형의 오차항을 의미하며 원인은 알려져 있지 않음
-평균이 0이면 가우시안 백색잡음
시계열 모형
(1)자기회귀(AR) 모형
-자기자신의 과거 값이 미래를 결정하는 모형
-부분자기상관함수(PACF)를 활용하여 p+1 시점 이후 급격 감소하면 AR(p) 모형 선정
(2)이동평균(MA) 모형
-이전 백색잡음들의 선형결합으로 표현되는 모형
-자기상관함수(ACF)를 활용하여 q+1 시차 이후 급격히 감소하면 MA(q) 모형 선정
(3)자기회귀누적이동편균(ARIMA) 모형
-AR 모형과 MA 모형의 결합
-ARIMA(p, d, q)
1)p와 q는 AR모형과 MA모형이 관련 있는 차수
2)d는 정상화시에 차분 몇 번 했는지 의미
3)d=0이면, ARMA 모델
4)p=0이면, IMA(d, q) 모델
5)q=0이면, ARI(p, d) 모델
분해시계열(자주 나옴)
-시계열에 영향을 주는 일반적인 요인을 시계열에서 분리해 분석하는 방법
(1)추세 요인: 장기적으로 증가, 감소하는 추세
(2)계절 요인: 계절과 같이 고정된 주기에 따라 변화
(3)순환 요인: 알려지지 않은 주기를 갖고 변화(경제 전반, 특정 산업)
(4)불규칙 요인: 위 3가지로 설명 불가한 요인
->'추운 계절의 순환이 불규칙하다'
3.정형 데이터 마이닝
데이터 마이닝 개요
데이터 마이닝
-방대한 데이터 속에서 새로운 규칙, 패턴을 찾고 예측을 수행하는 분야
데이터 마이닝의 유형
(1)지도학습: 정답이 있는 데이터를 활용
-인공신경망, 의사결정트리, 회귀분석, 로지스틱회귀
->'인공의사회귀'
(2)비지도학습: 정답이 없는 데이터들 사이의 규칙을 파악
-군집분석, SOM, 차원축소, 연관분석
과대적합과 과소적합
(1)과대적합: 모델이 지나치게 데이터를 학습하여 매우 복잡해진 모델 (규제를 가해야함)
(2)과소적합: 데이터를 충분히 설명하지 못하는 단순한 모델
데이터 분할
-과대적합과 과소적합을 방지하고, 데이터가 불균형한 문제를 해결하기 위해 사용
(1)분할된 데이터 셋 종류
1)훈련율(Training Set): 모델을 학습하는데 활용(50%)
2)검증용(Validation Set): 모델의 과대, 과소 적합을 조정하는데 활용(30%)
3)평가용(Test Set): 모델을 평가하는데 활용(20%)
(2)분할된 데이터의 학습 및 검증 방법
1)홀드아웃: 훈련용과 평가용 2개의 셋으로 분할
2)K-fold 교차검증: 데이터를 k개의 집단으로 구분하여 k-1개 학습, 나머지 1개로 평가
3)LOOCV: 1개의 데이터로만 평가, 나머지로 학습
4)부트스트래핑: 복원추출을 활용하여 데이터 셋을 생성, 데이터 부족, 불균형 문제 해소
분류분석
로지스틱 회귀분석
-종속변수가 범주형 데이터를 대상으로 성공과 실패 2개의 집단을 분류하는 문제에 활용
(1)오즈(Odds)
-성공할 확률과 실패할 확률의 비
-Odds= 성공확률(P)/실패확률(1-P)
(2)로짓(logit) 변환
-오즈에 자연로그(자연상수 e가 밑)를 취하는 작업
-독립변수 X가 n증가하면 확률이 만큼 증가
의사결정트리(Decision Tree)
-여러 개의 분리 기준으로 최종 분류 값을 찾는 방법
(1)분류(범주형)에서의 분할 방법
1)CHAID 알고리즘: 카이제곱 통계량
2)CART 알고리즘: 지니지수 활용
3)C4.5/C5.0 알고리즘: 엔트로피지수 활용
(2)회귀(연속형)에서의 분할 방법
1)CHAID 알고리즘: ANOVA F통계량
2)CART 알고리즘: 분산감소량

(3)학습간 규제
1)정지규칙
-분리를 더 이상 수행하지 않고 나무의 성장을 멈춤
2)가지치기
-일부 가지를 제거하여 과대적합을 방지
앙상블
-여러 개의 예측 모형들을 조합하는 기법으로 전체적인 분산을 감소시켜 성능 향상이 가능
(1)보팅(Voting)
-다수결 방식으로 최종 모델을 선택
(2)배깅(Bagging)
-복원추출에 기반을 둔 붓스트랩을 생성하여 모델을 학습한 후에 보팅으로 결합
-복원추출을 무한히 반복할 때 특정 하나의 데이터가 선택되지 않을 확률: 36.8%
(3)부스팅(Boosting)
-잘못된 분류 데이터에 큰 가중치를 주는 방법, 이상치에 민감
-종류: AdaBoost, GBM, XGBoost, Light GBM
(4)랜덤포레스트
-배깅에 의사결정트리를 추가하는 기법으로 성능이 좋고 이상치에 강한 모델
인공신경망
-인간의 뇌 구조를 모방한 퍼셉트론을 활용한 추론모델
(1)구조
1)단층 신경망: 입력층과 출력층으로 구성(단일 퍼셉트론)
2)다층 신경망: 입력층과 출력층 사이에 1개 이상의 은닉층 보유(다층 퍼셉트론)
-은닉층 수는 사용자가 직접 설정
(2)활성화 함수
-인공신경망의 선형성을 극복
1)시그모이드 함수
-0 ~ 1 사이의 확률 값을 가지며, 로지스틱 회귀 분석과 유사
2)소프트맥스 함수
-출력 값이 여러 개로 주어지고 목표 데이터가 다범주인 경우 활용
3)하이퍼볼릭 탄젠트(Tanh) 함수
--1 ~ 1 사이 값을 가지며, 시그모이드 함수의 최적화 지연을 해결
4)ReLU 함수
-기울기 소실문제를 극복, max(0,x)
(3)학습방법
1)순전파(피드포워드): 정보가 전방으로 전달
2)역전파 알고리즘: 가중치를 수정하여 오차를 줄임
3)경사하강법: 경사의 내리막길로 이동하여 오차가 최소가 되는 최적의 해를 찾는 기법
4)기울기 소실 문제
-다수의 은닉층에서 시그모이드 함수 사용 시, 학습이 제대로 되지 않는 문제
기타 분류모델
(1)KNN: 거리기반으로 이웃에 많은 데이터가 포함되어 있는 범주로 분류
(2)나이브베이즈: 나이브(독립), 베이즈 이론을 기반으로 범주에 속할 확률 계산
(3)SVM: 선형이나 비선형 분류, 회귀 등에서 활용할 수 있는 다목적 모델
분류모델 평가지표(지표 계산 무조건 나옴)
(1)오분류표
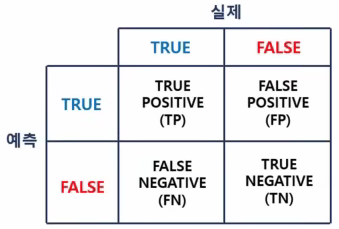
->예측과 실제가 같으면 TRUE, 예측이 TRUE면 POSITIVE
(2)평가지표
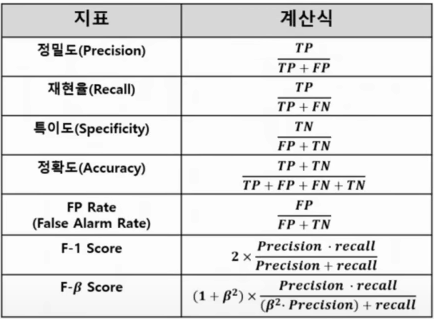
-재현율(Recall)은 민감도(Sensitivity), TP Rate, Hit Rate라고도 함
-F-1 Score는 Precision과 Recall의 조화평균
-Precision과 Recall은 Trade-Off 관계
(3)ROC 커브
-가로축을 1-특이도(FPR), 세로축을 민감도(TPR)로 두어 시각화한 그래프
-그래프 면적이 클수록(1에 가까울수록) 모델의 성능이 좋다고 평가(면적이 0.5가 가장 안좋음)
(4)이익도표(Lift chart)
-임의로 나눈 각 등급별로 반응검출율, 반응률, 리프트 등의 정보를 산출하여 나타내는 도표
-향상도 곡선: 이익도표를 시각화한 곡선
군집분석
군집분석
-비지도 학습으로 데이터들 간 거리나 유사성을 기준으로 군집을 나누는 분석
거리측도
(1)연속형 변수
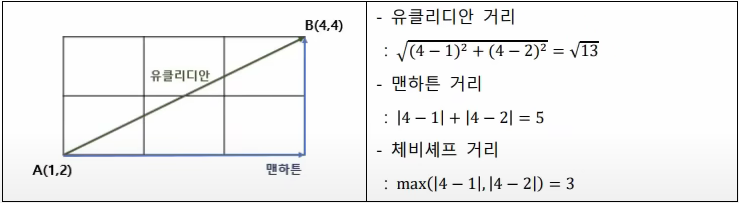
-유클리디안 거리: 두 점 사이의 직선 거리
-맨하튼 거리: 각 변수들의 차이의 단순 합
-체비셰프 거리: 변수 거리 차 중 최댓값
-표준화 거리: 유클리디안 거리를 표준편차로 나눔
-민코우스키 거리: 유클리드, 맨하튼 거리를 일반화한 거리
-마할라노비스 거리: 표준화 거리에서 변수의 상관성 고려
(2)범주형 변수
-자카드 유사도, 코사인 유사도
->'맨체스터 유나이티드' '자코'
실루엣 계수
-군집분석을 평가하는 지표로서 같은 군집간 가깝고, 다른 군집간 먼 정도를 판단(-1 ~ 1)
(1로 갈수록 좋은거)
계층적 군집분석
(1)거리측정 방법
1)최단 연결법(단일 연결법): 군집간 가장 가까운 데이터
2)최장 연결법(완전 연결법): 군집간 가장 먼 데이터
3)평균 연결법: 군집의 모든 데이터들의 평균
4)중심 연결법: 두 군집의 중심
5)와드 연결법: 두 군집의 편차 제곱합이 최소가 되는 위치
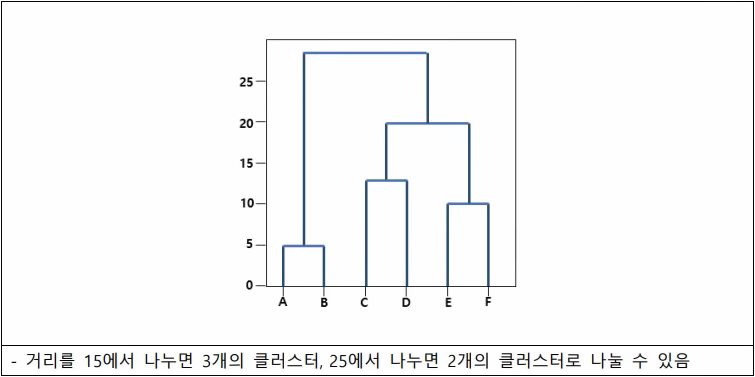
(2)덴드로그램
-계층적 군집화를 시각적으로 나타내는 Tree모양의 그래프
K평균 군집화(K-means Clustering)
-비계층적 군집화 방법으로 거리기반
(1)특징
-안정된 군집은 보장하나 최적의 보장은 어려움
-한번 군집에 속한 데이터는 중심점이 변경되면 군집이 변할 수 있음
(2)과정
1)군집의 개수 K개 설정
2)초기 중심점 설정
3)데이터들을 가장 가까운 군집에 할당
4)데이터의 평균으로 중심점 재설정
5)중심점 위치가 변하지 않을 때까지 3), 4)번 과정 반복
(3)K-medoids 군집화
-K평균 군집화의 이상치에 민감함을 대응하기 위한 군집방법
-일반적으로 실현된 것이 PAM(Partitioning Around Medoid)
혼합분포군집
-EM 알고리즘 활용
(1)E-Step
1단계) 초기 파라미터 값 임의 설정
2단계) 파라미터 값 활용하여 기댓값 계산
(2)M-Step
3단계) 기댓값으로부터 확률분포의 파라미터 값 추정
4단계) 2단계부터 반복 수행
SOM(자기 조직화 지도)
-차원축소와 군집화를 수행하여 고차원 데이터를 시각화하는 기법
(1)구성: 은닉층 없이 입력층과 출력층으로만 구성
(2)특징
-인공신경망과 달리 순전파 방식만 사용
-완전연결의 형태
-경쟁층에 표시된 데이터는 다른 노드로 이동 가능
-입력변수의 위치 관계를 그대로 보존
연관분석
연관분석
-항목들간의 조건-결과로 이루어지는 패턴을 발견하는 기법(장바구니 분석)
(1)특징
-결과가 단순하고 분명(IF ~ THEN ~)
-품목 수가 증가할수록 계산량이 기하급수적으로 증가
-Apriori 알고리즘을 활용하여 연관분석을 수행
(2)순차패턴
: 연관분석에 시간 개념을 추가하여 품목과 시간에 대한 규칙을 찾는 기법
연관분석의 지표
(1)지지도: N(A∩B)/전체 = P(A∩B)
-A와 B 두 품목이 동시에 포함된 거래 비율
(2)신뢰도: P(A∩B)/P(A)
-A 품목이 거래될 때 B품목도 거래될 확률(조건부 확률)
(3)향상도: P(A∩B)/P(A)P(B)
-A 품목과 B 품목의 상관성
(향상도 > 1: 양의 상관관계
향상도 = 1: 상관없음,
향상도 < 1: 음의 상관관계)
->'지신향'
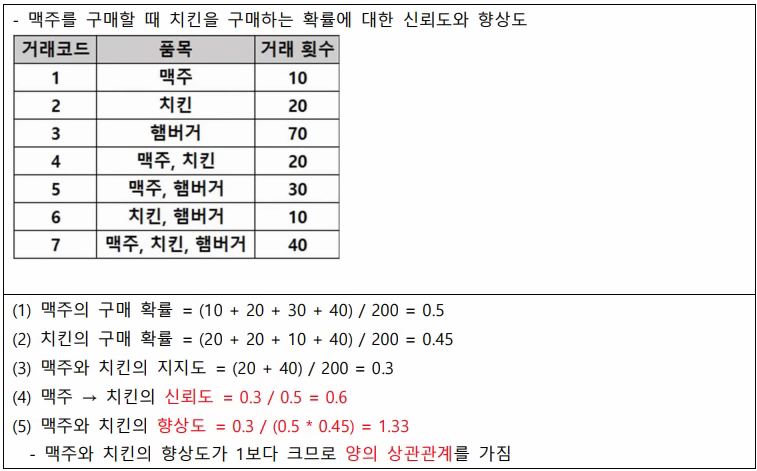
맥주를 구매할 때 치킨을 구매할 확률이 높고, 치킨을 구매할 때 맥주를 구매할 확률이 높다.
[참고문헌]
https://bookk.co.kr/bookStore/65c2003025cad6232f26b446
