알고리즘의 효율 분석

시간복잡도란 

알고리즘이 문제를 해결하는 데 걸리는 시간을 입력 크기에 따라 수학적으로 표현한것이다.
쉽게 말하면, 입력 데이터가 많아질수록(입력 크기  n ), 알고리즘이 얼마나 오래 걸리는지를 나타내는 척도이다.

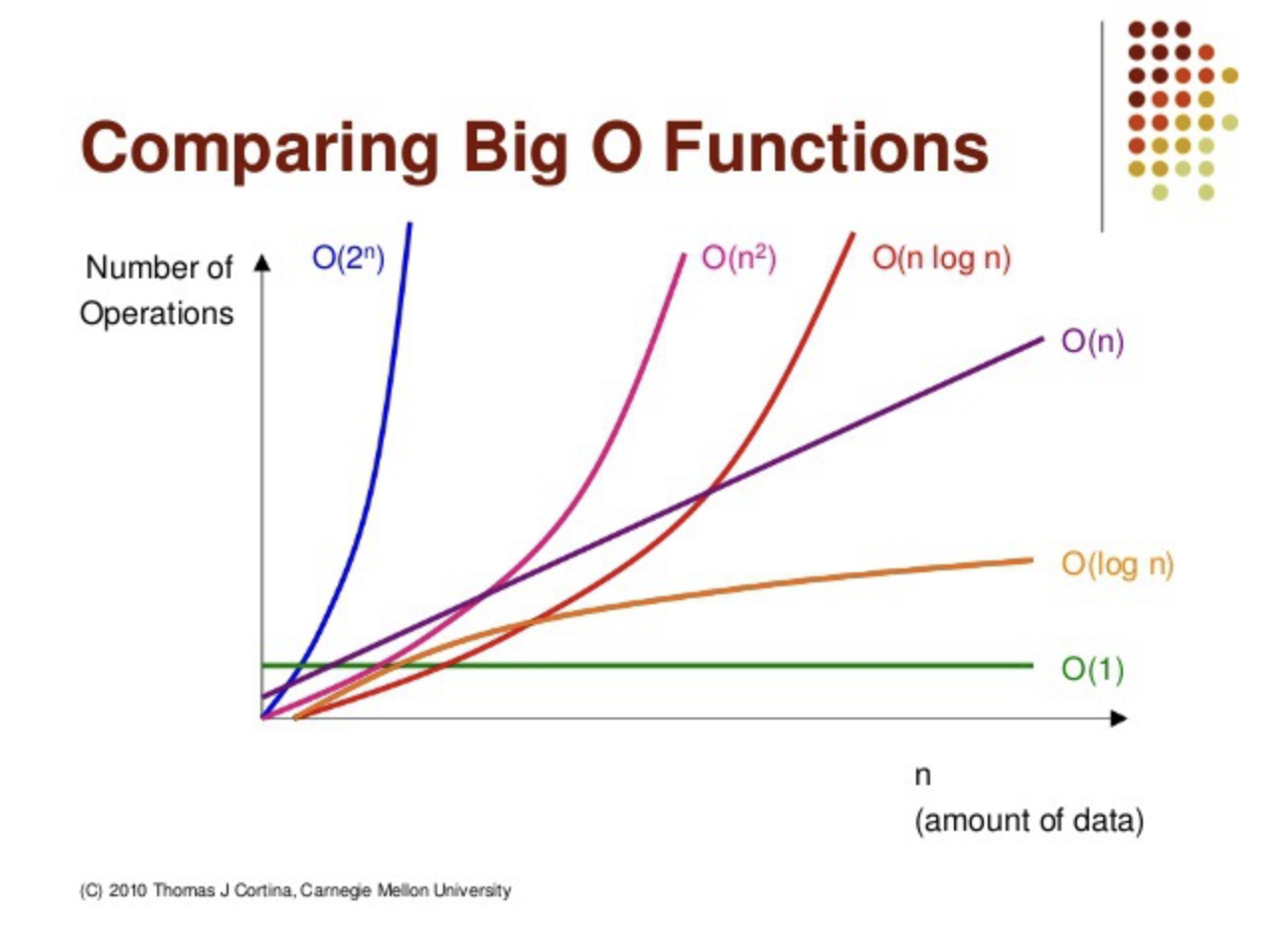
X축 (n): 입력 크기 → 처리해야 할 데이터의 양.
Y축 (Number of Operations): 알고리즘이 실행되기 위해 필요한 연산의 횟수.

$O(1)$ = 상수 시간

서랍 안에서 첫 번째 칸에 물건이 항상 있는 경우
물건이 어디에 있는지 정확히 알고 있으니 **한 번에 찾을수 있다

입력 크기(서랍 칸 수)가 아무리 많아도 시간이 변하지 않음.

$O(log n)$ = 로그 시간

물건이 정렬된 칸 안에 있을 때, 중간부터 확인하며 찾는 경우
예를 들어, 100칸 중 물건을 찾으려면 중간(50번째 칸)을 먼저 열어보고, 물건이 왼쪽에 있으면 오른쪽 절반은 무시.

물건이 있는 칸의 범위를 반씩 줄여가며 찾음.

$O(n)$ = 선형 시간

서랍에 물건이 어딘가 들어있지만, 정렬이 안 되어 있음.
첫 번째 칸부터 마지막 칸까지 모두 확인해야 함.
한 칸씩 전부 열어야해서, 서랍 칸이 많을수록 시간이 오래 걸림.

서랍 칸 수가 많아질수록 시간도 비례해서 늘어남.

$O(n log n)$ = 선형 로그 시간

서랍 안의 물건을 꺼내 정리하고, 필요한 물건을 찾는 경우
먼저 서랍에 있는 물건을 반씩 나누며 정리하고, 그 다음 물건을 효율적으로 찾아봄.
정리 + 찾기 작업이 합쳐져 있어 O(n) 보다는 느리지만 효율적이다

정리와 찾기를 반복하므로 시간이 조금 더 걸림.

$O(2^n)$ = 이차 시간

서랍에 물건이 여러 개 있는데, 모든 물건끼리 비교해야 하는 경우
예를 들어, 물건을 크기 순으로 정렬하려고 모든 물건을 서로 비교.
n개의 물건이 있을 때, 모든 물건과 짝을 이루어 비교하니 시간이 많이 걸림.

서랍 칸 수가 많아질수록 시간이 기하급수적으로 늘어남.

$O(n^2)$ = 지수 시간

서랍에 있는 모든 물건을 꺼내, 가능한 모든 조합을 만드는 경우.
예를 들어, “서랍에서 어떤 물건들을 조합해서 새로운 물건을 만들 수 있을까?“를 계산.
모든 조합을 확인해야 하므로 칸 수가 많아질수록 시간이 폭발적으로 증가.

현실적으로 비효율적임.

---

로그함수란?

로그 함수는 다음과 같은 질문을 풀기 위한 도구이다.

“밑(base)을 몇 번 곱해야 결과 값이 나오는가?”

수식 형태

$\log_b$ x = y

여기서:

• b : 밑(base) → 몇을 기준으로 곱할지 정함.

• x : 결과 값 → 곱해서 얻는 숫자.

• y : 지수 → 몇 번 곱했는지를 의미.

로그 함수의 그래프

로그 함수의 특징은 입력 크기 n 이 커질수록 증가 속도가 느려지는 것이다.

$\log_2 2 = 1$
$\log_2 4 = 2$
$\log_2 8 = 3$
$\log_2 16 = 4$

데이터가 커져도 증가율이 점점 완만해진다.

---

결론적으로 시간복잡도는 실제 실행 시간을 예측하는 도구일 뿐, 정확한 시간을 알 필요는 없다
현실에서는 데이터 크기, 컴퓨터 성능, 언어의 구현 등 여러 요인으로 실행 시간이 달라지기 때문에, 시간복잡도는 대략적인 경향만 알려주는 역할이다

현실 문제는 시간복잡도 외에도 고려할 게 많음

• 시간복잡도가 낮다고 무조건 좋은 알고리즘은 아니다.

• 메모리 사용량: 시간복잡도가 빠른 알고리즘이라도 메모리를 많이 쓰면 비효율적일 수 있다.

• 현실 데이터 크기: 입력 데이터 크기가 작다면  $O(n^2)$  알고리즘도 충분히 빠를 수 있다.

• 코드 구현 복잡도:  $O(log n) 이  O(n)$ 보다 효율적이어도, 코드가 너무 복잡하면 유지보수 비용이 클 수 있다.

시간복잡도는 대략적인 가이드로 충분하다.