링크 : https://www.cv-foundation.org/openaccess/content_iccv_2015/papers/Chen_An_Efficient_Statistical_ICCV_2015_paper.pdf

(참고) 이 논문은 2015년에 발표된 것으로, 현재 기준에서는 최신 기술이라고 보기 어렵습니다. 본문에서 언급된 "최근" 또는 "최신"이라는 표현은 모두 당시 기준이며, 현재의 기술 흐름과는 다를 수 있습니다.

---

1. 서론

이 논문은 단일 영상에서 가법적 영평균 가우시안 노이즈(additive zero-mean Gaussian noise)의 노이즈 레벨을 추정하는 문제를 다룹니다. 노이즈 레벨은 영상 잡음 제거(image denoising), 광학 흐름(optical flow), 영상 분할(image segmentation), 초해상도(super resolution) 등 다양한 컴퓨터 비전 알고리즘에 필수적인 파라미터입니다. 그러나 실제 상황에서는 영상의 노이즈 레벨을 알 수 없는 경우가 많으며, 특히 텍스처가 풍부한 영상의 경우 정확한 노이즈 레벨 추정은 여전히 어려운 과제로 남아 있습니다.

기존의 노이즈 추정 방법들([2, 17, 13, 20, 24])은 처리할 영상에 충분한 양의 평탄 영역(flat areas)이 포함되어 있다는 가정을 기반으로 합니다. 하지만 이는 자연 영상 처리에서는 항상 적용되는 가정이 아닙니다. 최근 제안된 최신 알고리즘들([19, 23])은 이러한 가정이 필요 없다고 주장하지만, 다음과 같은 두 가지 약점을 가지고 있습니다.

1. 첫째, [19]에서 언급했듯이, 저랭크(low-rank) 패치 선택의 수렴성 및 성능이 이론적으로 보장되지 않으며 경험적으로도 높은 정확도를 보이지 않습니다.

2. 둘째, 본 논문의 2.2절에서 이론적으로 설명하듯이, 이들 방법은 선택된 저랭크 패치의 공분산 행렬의 가장 작은 고유값(eigenvalue)을 노이즈 추정 결과로 사용하기 때문에 처리된 영상의 노이즈 레벨을 과소평가(underestimate)하는 경향이 있습니다.

이러한 문제들을 해결하기 위해, 본 논문은 새로운 노이즈 레벨 추정 알고리즘을 제안합니다. 이 연구는 노이즈가 없는 영상에서 추출된 패치들이 주변 공간(ambient space)에 균일하게 분포하기보다 종종 저차원 부분공간(low-dimensional subspace)에 존재한다는 관찰에 기반합니다.

이러한 특성은 부분공간 클러스터링(subspace clustering) 방법([8, 29])에서 널리 활용되었습니다. 이 저차원 부분공간은 주성분 분석(Principal Component Analysis, PCA)을 통해 학습될 수 있습니다. 본 논문의 2.1절에서 분석하듯이, 노이즈 분산(noise variance)은 잉여 차원(redundant dimensions)의 고유값으로부터 추정될 수 있습니다. 이러한 방식으로, 노이즈 레벨 추정 문제는 PCA를 위한 잉여 차원을 선택하는 문제로 재구성됩니다.

(참고) 잉여 차원의 의미: 논문에서는 깨끗한 이미지 패치들이 사실상 "저차원 부분 공간(low-dimensional subspace)"에 놓여 있다고 가정합니다. 이는 이미지 패치에 포함된 실제 정보(예: 이미지의 구조, 텍스처 등)는 전체 패치의 픽셀 수(고차원)보다 훨씬 적은 수의 차원으로도 충분히 설명될 수 있다는 뜻입니다.

이 문제는 통계학 및 신호 처리 분야에서 모델 선택(model selection) 문제로 연구되어 왔습니다([10, 15, 21, 28]). 그러나 이들 방법은 관측된 신호를 표현하기 위해 더 적은 잠재 구성요소(latent components)를 사용하는 데 중점을 두기 때문에, 신호 구성요소를 노이즈로 간주하여 영상 노이즈를 과대평가(overestimate)하는 결과를 초래합니다.

본 논문에서는 잉여 차원의 고유값이 동일한 분포를 따르는 확률 변수라는 통계적 속성을 활용하여 이 문제를 해결하는 효과적인 방법을 제안합니다. 이는 2.2절에서 입증되었으며, 제안된 방법은 주성분(principal dimensions)의 수가 특정 임계값보다 작을 때 정확한 노이즈 추정을 달성할 것으로 2.3절에서 입증됩니다.

본 논문의 주요 기여는 다음과 같이 요약할 수 있습니다:

• 노이즈 레벨 $\sigma^2$와 패치의 공분산 행렬 고유값 사이의 통계적 관계를 최초로 추정합니다.

• 고유값으로부터 노이즈 레벨 $\sigma^2$을 추정하는 비모수(nonparametric) 알고리즘을 제안하며, 이 알고리즘의 성능은 이론적으로 보장됩니다. 경험적으로 본 방법은 가장 견고하며 대부분의 경우 노이즈 레벨 추정에서 최고의 성능을 달성합니다. 또한, 본 방법은 가장 적은 실행 시간을 소모하며 [19, 23]보다 거의 8배 빠릅니다.

• 디노이징 알고리즘 BM3D가 본 알고리즘으로 추정된 노이즈 분산을 사용할 때 최적의 성능을 달성함을 추가로 입증합니다.

2. 관련 연구

기존의 많은 노이즈 추정 방법들([2, 17, 13, 20, 24])은 영상 내에 충분한 평탄 영역이 존재한다는 가정에 의존합니다. 이 가정은 자연 영상에서 항상 유효하지 않아 텍스처가 풍부한 영상에서 정확한 추정을 어렵게 합니다.

(관련연구) 노이즈 추정 방법들

• [2]: Segmentation of images based on intensity gradient information

  • 저자: R. Bracho, A. C. Sanderson
  • 설명: 1985년에 발표된 이 논문은 이미지의 강도 기울기 정보(intensity gradient information)를 기반으로 한 이미지 분할(Segmentation)에 대해 다룹니다.

• [17]: Refined filtering of image noise using local statistics

  • 저자: Jong-Sen Lee
  • 설명: 1981년 논문으로, 지역 통계값(local statistics)를 사용하여 이미지 노이즈를 정제하는 필터링 방법에 초점을 맞춥니다.

• [13]: Fast Noise Variance Estimation

  • 저자: John Immerkær
  • 설명: 1996년 논문으로, 빠르고 효율적인 노이즈 분산 추정 방법을 제안합니다.

• [20]: A fast parallel algorithm for blind estimation of noise variance

  • 저자: P. Meer, J. Jolion, A. Rosenfeld
  • 설명: 1990년 논문으로, '블라인드' 노이즈 분산 추정을 위한 빠르고 병렬적인 알고리즘을 제안합니다.

• [24]: Estimation of image noise variance

  • 저자: K. Rank, M. Lendl, R. Unbehauen
  • 설명: 1999년 논문으로, 이미지 노이즈 분산 추정에 대한 연구입니다.

최근의 최첨단 방법인 [19]와 [23]은 평탄 영역이 없는 영상에서도 노이즈 레벨을 정확하게 추정할 수 있다고 주장합니다. 그러나 이들은 저랭크 패치의 공분산 행렬에서 가장 작은 고유값 $\lambda_r$을 노이즈 추정 결과로 사용합니다.

본 논문의 2.2절에서 이론적으로 분석했듯이, 이 접근 방식은 처리된 영상의 노이즈 레벨을 일관되게 과소평가하는 문제를 야기합니다. 이는 잉여 차원(redundant space)의 고유값이 가우시안 분포를 따른다는 점과, 정렬된 고유값의 기대값이 특정 분포를 따른다는 점(Theorem 1, Blom의 정리)을 통해 설명됩니다. 특히, 잉여 차원(redundant space)의 수가 1보다 클 때 가장 작은 고유값의 기대값은 실제 노이즈 레벨보다 작아집니다.

(관련연구) 노이즈 추정 최신 방법들

• [19]: Single-Image Noise Level Estimation for Blind Denoising

  • 저자: Xinhao Liu, Masayuki Tanaka, M. Okutomi
  • 설명: 2013년 발표된 이 논문은 단일 이미지로부터 '블라인드' 디노이징을 위한 노이즈 레벨을 추정하는 방법을 다룹니다.

• [23]: Image Noise Level Estimation by Principal Component Analysis

  • 저자: Stanislav Pyatykh, J. Hesser, Lei Zheng
  • 설명: 역시 2013년에 발표된 이 논문은 주성분 분석(PCA)을 활용하여 이미지 노이즈 레벨을 추정하는 방법을 제안합니다.

또한, 노이즈 레벨 추정을 차원 선택 문제로 재해석하여 PCA의 잉여 차원(redundant space)을 선택하는 접근 방식은 통계 및 신호 처리 분야의 모델 선택 문제([10, 15, 21, 28])와 유사합니다. 그러나 이러한 기존 방법들은 관측된 신호를 표현하기 위해 더 적은 잠재 구성요소를 사용하는 데 초점을 맞추기 때문에, 신호 구성요소(signal components)를 노이즈로 간주하여 영상 노이즈를 과대평가하는 경향이 있습니다.

(관련연구) 통계 및 신호 처리 분야의 모델 선택 문제

• [10]: The Optimal Hard Threshold for Singular Values is $4/\sqrt {3}$

  • 저자: M. Gavish, D. L. Donoho
  • 설명: 2014년 발표된 이 논문은 특이값(singular values)에 대한 최적의 하드 임계값(hard threshold)을 다룹니다.

• [15]: Non-Parametric Detection of the Number of Signals: Hypothesis Testing and Random Matrix Theory

  • 저자: S. Kritchman, B. Nadler
  • 설명: 2009년 논문으로, 가설 검정(Hypothesis Testing)과 무작위 행렬 이론(Random Matrix Theory)을 사용하여 신호의 개수를 비모수적으로 탐지하는 방법을 제시합니다.

• [21]: Perfect Dimensionality Recovery by Variational Bayesian PCA

  • 저자: S. Nakajima, R. Tomioka, M. Sugiyama, S. D. Babacan
  • 설명: 2012년 논문으로, Variational Bayesian PCA를 통해 차원(dimensionality)을 완벽하게 복구하는 방법을 제시합니다.

• [28]: Dimension Estimation in Noisy PCA with SURE and Random Matrix Theory

  • 저자: M. O. Ulfarsson, V. Solo
  • 설명: 2008년 논문으로, 노이즈가 있는 PCA에서 SURE(Stein's Unbiased Risk Estimator)와 무작위 행렬 이론을 사용하여 차원 추정을 다룹니다.

본 논문은 이러한 기존 방법들의 한계를 극복하기 위해, 잉여 차원(redundant space)의 고유값이 특정 통계적 분포(가우시안 분포)를 따른다는 점을 활용하여 노이즈를 보다 정확하게 추정하고, 가장 작은 고유값 대신 잉여 차원 전체의 통계적 특성을 사용하여 과소평가 문제를 해결합니다.

---

3. 방법론

본 논문의 방법론은 영상 패치(patch)를 기반으로 하며, 패치의 공분산 행렬의 고유값 분석을 통해 노이즈 레벨을 추정합니다.

3.1. 패치 분해 및 노이즈 모델링

관측된 영상 $I$는 $s$개의 패치 집합 $\mathbf{X}_s = \{\mathbf{x}_t\}_{t=1}^s \in \mathbb{R}^{r \times s}$로 분해될 수 있습니다.

관측된 영상 $I$는 $s$개의 패치 집합 $\mathbf{X}_s = \{\mathbf{x}_t\}_{t=1}^s$로 나눌 수 있다.

• 이미지를 작은 조각들(패치) 로 나눕니다.
• 각 패치는 $d \times d \times c$ 크기 (예: 8×8×3)이고, 이를 벡터 $\mathbf{x}_t \in \mathbb{R}^{r \times 1}$로 펴서 사용합니다.
• 전체 이미지는 이렇게 벡터화된 패치들의 집합 $\mathbf{X}_s \in \mathbb{R}^{r \times s}$로 표현됩니다.

임의의 관측 패치$\mathbf{x}_t$는 다음과 같이 분해됩니다:

$\mathbf{x}_t = \hat{\mathbf{x}}_t + \mathbf{e}_t \quad (1)$

• $\mathbf{x}_t$: 실제 관측된 패치 (노이즈 포함)
• $\hat{\mathbf{x}}_t$: 노이즈가 없는 진짜 패치
• $\mathbf{e}_t$: 노이즈만 따로 분리한 성분

가정

• 노이즈 $\mathbf{e}_t$는 평균이 0이고, 분산이 $\sigma^2$인 가우시안 노이즈입니다.

• 수학적으로는 다음과 같이 표현됩니다:

  $\mathbf{e}_t \sim \mathcal{N}_r(0, \sigma^2 \mathbf{I})$
  • 노이즈는 랜덤하지만, 전체적으로 보면 정규분포를 따르는 무작위 잡음입니다.
  • 각 픽셀은 독립적으로 노이즈가 섞여 있고, 그 세기는 $\sigma^2$로 표현됩니다.

결국, 영상의 노이즈 수준을 추정한다는 것은
패치 집합 $\mathbf{X}_s$ 에서 노이즈 분산 $\sigma^2$ 를 추정하는 것과 같습니다.

즉, 많은 패치들을 분석해서 그 안에 섞여 있는 노이즈의 평균적인 세기(분산) 를 계산하는 것이 이 논문의 핵심입니다.

---

3.2. 고유값과 노이즈 분산의 관계

이미지의 패치들이 저차원 선형 부분공간에 놓여 있다고 가정하면, 각 관측 패치 $\mathbf{x}_t$는 다음과 같이 표현됩니다:

• $\mathbf{A} \in \mathbb{R}^{r \times m}$: 부분공간을 정의하는 직교 기저 행렬
• $\mathbf{y}_t$: 부분공간 상의 좌표
• $\mathbf{e}_t$: 평균 0, 분산 $\sigma^2$의 가우시안 노이즈

이 모델은 관측된 패치가 신호 성분과 노이즈 성분의 합으로 구성된다는 것을 의미합니다.

🔄 회전 행렬을 통한 성분 분리

공분산 행렬 $\Sigma_{\mathbf{x}}$의 고유값 분해를 통해 얻은 회전 행렬 $\mathbf{R} = [\mathbf{A}, \mathbf{U}]$를 사용하면, 패치 $\mathbf{x}_t$를 다음과 같이 분리할 수 있습니다:

• 상단: 신호 성분 + 일부 노이즈
• 하단: 노이즈만 포함된 성분 → 잉여 차원

📊 고유값과 노이즈 분산

이미지 패치들의 공분산 행렬 $\Sigma_{\mathbf{x}}$를 고유값 분해하면, 회전 행렬 $\mathbf{R}$을 통해 다음과 같이 대각화됩니다:

여기서 각 고유값 $\lambda_i$는 해당 차원의 데이터 분산을 나타냅니다.

• 신호와 노이즈 차원의 구분
  • 이미지 패치들은 실제로는 저차원 선형 부분공간에 집중되어 있다고 가정합니다.
  • 이때:
    • 신호가 포함된 차원에서는 $\lambda_i > \sigma^2$
      → 구조적 정보가 존재하므로 분산이 큼
    • 노이즈만 포함된 잉여 차원에서는 $\lambda_i \approx \sigma^2$
      → 구조가 없고, 오직 노이즈만 존재하므로 분산이 작고 일정함

이러한 특성은 회전 행렬 $\mathbf{R}$을 통해 신호와 노이즈 성분이 분리되었기 때문에 가능해집니다.

• 노이즈 분산 추정 방법

  • 노이즈만 포함된 차원들의 고유값은 통계적으로 노이즈 분산 $\sigma^2$ 를 중심으로 한 정규분포를 따릅니다.
  • 따라서, 이들 고유값의 평균을 취하면 노이즈 분산을 추정할 수 있습니다:
  $\sigma^2 \approx \frac{1}{r - m} \sum_{i=m+1}^{r} \lambda_i$
  • $r$: 전체 차원 수 (패치 벡터의 길이)
  • $m$: 신호가 포함된 차원 수
  • $r - m$: 노이즈만 포함된 잉여 차원 수

이 식은 작은 고유값들(노이즈 차원) 의 평균이 노이즈 분산의 통계적 추정치가 된다는 원리에 기반합니다.

---

3.3. 유한 가우시안 변수의 분산 및 과소평가 문제 분석

기존 연구 [19], [23]에서는 최소 고유값을 이미지 노이즈 분산 $\sigma^2$의 추정치로 사용했습니다. 하지만 실험 결과, 이 방식은 노이즈 수준을 지속적으로 과소평가하는 경향이 있음을 보여줍니다.

이를 설명하기 위해 논문에서는 Lemma 1과 Theorem 1을 제시합니다.

Lemma 1: 고유값의 통계적 분포

• 각 잉여 차원의 고유값 $\lambda_i$는 가우시안 노이즈 $\mathcal{N}(0, \sigma^2)$에서 유도된 확률 변수들의 제곱 평균으로 계산됩니다.
• 이 값은 $s$개의 샘플을 기반으로 하며, $s \to \infty$일 때 다음 분포로 수렴합니다:

• 즉, 고유값은 노이즈 분산을 중심으로 한 정규분포를 따르며, 이는 Monte Carlo 시뮬레이션으로도 검증됩니다.

Theorem 1: 최소 고유값의 기대값

• $n$개의 고유값이 정규분포 $\mathcal{N}(\sigma^2, \nu^2)$를 따른다고 할 때, 최소 고유값의 기대값은 다음과 같이 근사됩니다:

• 여기서 $\Phi^{-1}$는 표준 정규분포의 역누적함수, $\alpha = 0.375$, $\nu = \sqrt{\frac{2\sigma^4}{s}}$입니다.
• 이 식에 따르면, 최소 고유값의 기대값은 항상 $\sigma^2$보다 작게 나타나며, 잉여 차원의 수가 많을수록 과소평가 정도가 커집니다.

⚠️ 결론 및 한계

• 기존 방법([19], [23])은 최소 고유값을 노이즈 추정치로 사용했지만, 이는 통계적으로 과소평가될 수밖에 없는 구조입니다.
• 특히, 고차원 이미지나 패치 수가 많을수록 이 오차는 더 커지며, 정확한 노이즈 추정을 위해서는 고유값 전체 분포를 고려한 평균 기반 접근이 필요합니다.

---

3.4. 차원 선택 알고리즘

앞선 섹션에서 설명한 바와 같이, 노이즈 분산을 정확하게 추정하기 위해서는 노이즈만 포함된 고유값 집합 $\mathbf{S}_2$ 전체를 고려해야 합니다. 하지만 실제로는 신호가 포함된 차원 수 $m$ 를 사전에 알 수 없기 때문에, 이를 자동으로 추정하는 알고리즘이 필요합니다.

논문에서는 이를 해결하기 위해 상위 이상치(upper outliers) 를 기반으로 한 차원 선택 알고리즘을 제안합니다.

🧠 핵심 아이디어

• 고유값 집합 $\mathbf{S} = \{\lambda_1, \lambda_2, \ldots, \lambda_r\}$에서
  • 신호가 포함된 차원의 고유값은 평균보다 크고
  • 노이즈만 포함된 차원의 고유값은 평균과 중앙값이 거의 같음
• 따라서, 고유값 집합에서 평균이 중앙값보다 큰 경우, 상위 이상치가 존재한다고 판단하고
  • 가장 큰 고유값을 제거하며 반복
• 평균이 중앙값과 같아지는 순간, 신호 차원 제거 완료 → 잉여 차원만 남음

📐 Theorem 2: 평균과 중앙값의 관계

• $m > 0$일 때: 고유값 집합의 평균은 중앙값보다 큼
• $m = 0$ 또는 이상치가 없을 때: 평균과 중앙값이 같음
• 이 관계를 통해 신호 차원 수 $m$ 를 추정할 수 있음

⚙️ Algorithm 1: 영상 노이즈 레벨 추정

1. 입력 영상 $I$에서 $s$개의 패치를 추출
2. 평균 벡터 $\mu$ 계산
3. 공분산 행렬 $\Sigma$ 계산
4. 고유값 $\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_r$ 정렬
5. 반복문을 통해 고유값 집합의 평균과 중앙값 비교
6. 평균 = 중앙값이 되는 순간의 평균값을 $\tau$로 설정
7. 노이즈 표준편차 $\sigma = \sqrt{\tau}$ 반환

---

3.5. 구현 및 시간 복잡도

본 방법의 핵심 아이디어는 주성분 차원 $\mathbf{S}_1$의 고유값을 $\mathbf{S}$에서 제거함으로써 정확한 노이즈 분산을 얻는 것입니다. 위 Algorithm 1에 설명된 단계에 따라 시간 복잡도를 분석할 수 있습니다.

• $s$개의 $r$-차원 샘플을 갖는 $\mathbf{X}$집합을 생성하는 복잡도는 $O(sr)$입니다.

• 데이터셋 $\mathbf{X}$의 평균 벡터 $\mathbf{\mu}$ 및 공분산 행렬 $\mathbf{\Sigma}$를 계산하는 것은 각각 $O(sr)$ 및 $O(sr^2)$입니다.

• $\mathbf{\Sigma}$의 고유 분해는 $O(r^3)$입니다.

• 4단계의 정렬 과정은 $O(r \log r)$(혹은 $O(r^2)$if using selection sort as implied by loop)를 소비하며, 5-9단계의 확인 절차는 최악의 경우 $r$번 반복하며 각 반복에서 평균과 중앙값을 계산하므로 $O(r \cdot r) = O(r^2)$가 걸립니다.

• Algorithm 1의 $r^2$는 고유값 개수 $r$에 대해 $r$번 반복하며 매 반복마다 부분 집합의 평균을 계산하고, 중앙값을 찾는 데 $O(r)$가 걸리기 때문입니다.

따라서, 본 방법의 총 시간 복잡도는 $O(sr^2 + r^3)$이며, 이는 다항 시간(polynomial time)에 해결될 수 있음을 의미합니다.

---

4. 실험

제안된 노이즈 추정 알고리즘의 성능을 평가하기 위해 합성 노이즈 영상, 실제 노이즈 영상, 그리고 영상 복원 응용(BM3D) 에서의 효과를 실험적으로 검증했습니다. 비교 대상은 기존의 대표적인 노이즈 추정 방법 [19], [23]이며, 모든 실험은 동일한 환경(MATLAB R2013a, Intel i7 CPU)에서 수행되었습니다.

---

4.1 파라미터 설정

• 알고리즘에서 유일한 사전 설정 파라미터는 패치 크기 ( d ) 입니다.
• 패치 크기가 클수록 텍스처 표현에 유리하지만, 샘플 수 ( s )가 줄어들어 통계적 신뢰도가 낮아지고 실행 시간이 증가합니다.
• 본 논문에서는 패치 크기 ( d = 8 ) 을 기본값으로 사용하여 성능과 효율성의 균형을 맞췄습니다.

---

4.2 노이즈 레벨 추정 결과

4.2.1 TID2008 데이터셋

• 합성된 백색 노이즈를 추가한 영상에 대해 노이즈 수준을 추정
• 평가 지표:
  • Bias: 추정치의 정확도
  • Std: 추정치의 견고성
  • √MSE: 전체 성능

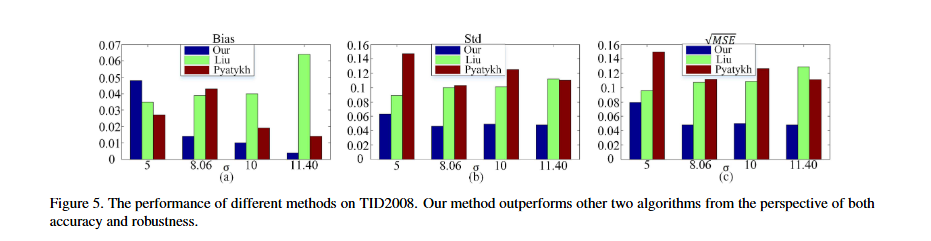
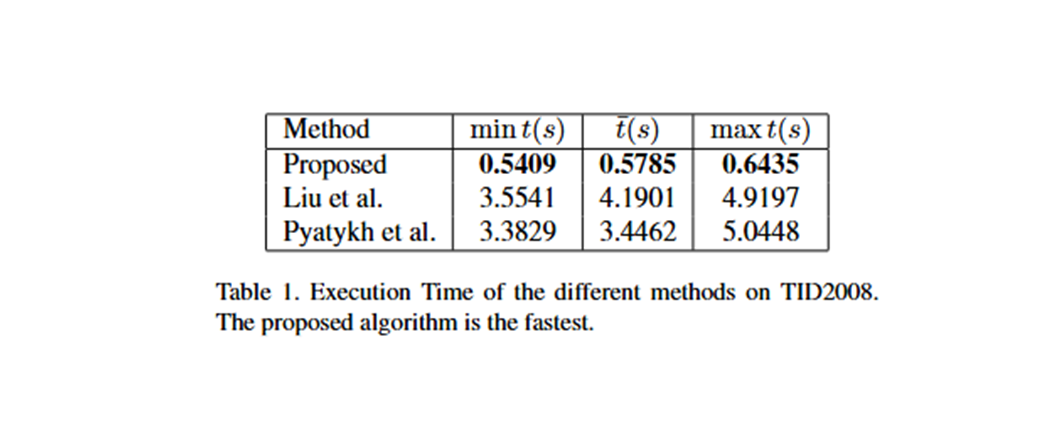
• 제안된 방법은 대부분의 경우 기존 방법보다 더 정확하고 견고한 추정을 보였으며, 실행 시간도 약 8배 빠름 (0.5초 vs 4초)

4.2.2 BSDS500 데이터셋

• 텍스처가 풍부한 영상에서의 성능을 평가
• 제안된 방법은 모든 지표에서 기존 방법보다 우수한 성능을 보였으며, Gavish의 방법보다도 더 낮은 MSE를 기록함

4.2.3 실제 노이즈 영상

• Nikon D5200으로 저조도 환경에서 촬영한 100개의 정적 장면 영상 사용
• 평균 영상을 기준으로 지상 진실 노이즈 분산을 계산
• 제안된 방법은 실제 노이즈 환경에서도 가장 정확한 추정 성능을 보임

---

4.3 영상 잡음 제거 응용

• 제안된 노이즈 추정치를 BM3D 알고리즘의 입력 파라미터로 사용
• TID2008 및 BSDS500 영상에서 BM3D 성능을 평가
• 결과적으로, 추정된 노이즈 수준을 사용한 BM3D의 성능은 실제 노이즈 수준을 사용한 경우와 거의 동일
• 이는 제안된 방법이 실제 디노이징 응용에도 매우 적합함을 보여줌

---

5. 토론

이 연구는 단일 노이즈 영상에서 노이즈 레벨을 효율적으로 추정하는 통계적 방법을 제안했습니다. 핵심적인 기여는 영상 패치의 공분산 행렬의 고유값과 노이즈 분산 사이의 통계적 관계를 심층적으로 분석한 것입니다. 특히, 이전의 최신 방법들이 가장 작은 고유값을 노이즈 추정치로 사용하여 노이즈 레벨을 과소평가하는 문제를 이론적으로 규명하고, 이를 Lemma 1과 Theorem 1을 통해 증명했습니다.

제안된 비모수 알고리즘은 이러한 과소평가 문제를 해결하기 위해, 잉여 차원 고유값의 통계적 특성(가우시안 분포)을 활용하여 이상치를 제거하고 실제 노이즈 분산을 추정합니다. Algorithm 1의 차원 선택 절차는 고유값 집합의 평균과 중앙값을 비교하여 이상치 존재 여부를 판단하며, 이는 Theorem 2에 의해 이론적으로 정당화됩니다.

실험 결과는 제안된 방법이 기존의 최신 알고리즘([19, 23])보다 훨씬 우수한 성능을 보임을 명확히 보여줍니다. TID2008과 BSDS500 데이터셋 모두에서 본 방법은 정확도, 견고성, 그리고 속도 면에서 뛰어났습니다. 특히, 텍스처가 풍부하여 노이즈 추정이 어려운 BSDS500 데이터셋과 실제 환경에서 촬영된 노이즈 영상에서 그 우수성이 더욱 두드러졌습니다. 실행 시간 측면에서, 본 방법은 기존 방법들보다 약 8배 빨라 실용적인 응용에 매우 적합합니다.

BM3D와 같은 데노이징 알고리즘에 본 방법으로 추정된 노이즈 레벨을 입력으로 사용했을 때, 참 노이즈 레벨을 사용했을 때와 거의 동일한 데노이징 성능을 달성했습니다. 이는 본 노이즈 추정 방법의 실용적 가치를 강력하게 뒷받침합니다.

본 연구의 한계점은 노이즈가 영평균 가법적 가우시안 분포를 따른다고 가정한 것입니다. 실제 환경에서의 노이즈는 더 복잡한 특성을 가질 수 있으며, 이는 향후 연구의 방향입니다.

---

6. 결론

본 논문에서는 단일 노이즈 영상으로부터 노이즈 분산을 자동으로 추정하는 효율적인 방법을 제안했습니다. 이 방법은 다양한 컴퓨터 비전 알고리즘에 매우 중요합니다. 제안된 방법의 성능은 이론적으로 보장되었으며, 두 가지 최신 방법과 비교하여 대부분의 경우 가장 적은 실행 시간으로 최고의 정확도를 달성함을 보여주었습니다.

읽어주셔서 감사합니다 :)