알고리즘: 피보나치 수열 구현하기

피보나치 수열

피보나치 수열은 다음과 같은 점화식으로 정의되는 수열이다.

피보나치 수열을 제 15항까지 나타낸다면 다음과 같다.

$n$	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$	$10$	$11$	$12$	$13$	$14$	$15$
$F_{n}$	$0$	$1$	$1$	$2$	$3$	$5$	$8$	$13$	$21$	$34$	$55$	$89$	$144$	$233$	$377$	$610$

피보나치 수열의 구현

피보나치 수열은 재귀 함수를 통해 구현 가능하다.

def fib(n: int) -> int:
	if n == 0 or n == 1: return n
    return fib(n - 1) + fib(n - 2)
    
fib(17)

위 코드를 직접 돌려보면, $n$을 $100$과 같이 큰 숫자를 넣기만 해도 굉장히 오래 걸리는 모습을 볼 수 있다.
어디서 오랜 시간이 소요되는걸까?

fib(5)를 구하기 위한 과정은 다음과 같다.

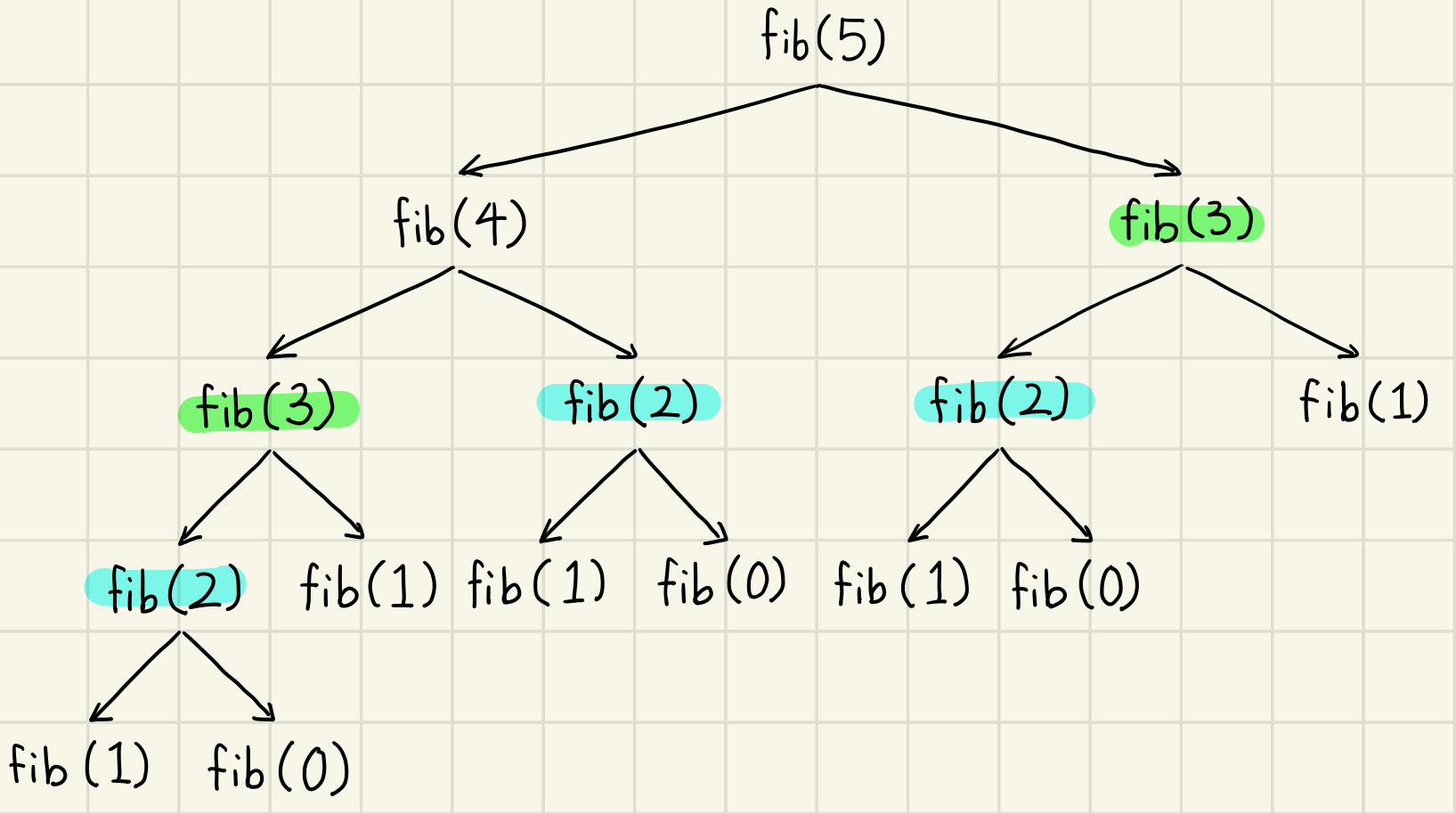
위 과정을 보면 fib(5)를 계산하기 위해 fib(3)은 두 번 호출되고, fib(2)는 세 번 호출된다.

즉, 하나의 노드 당 두 개의 자식 노드가 생성되고 있음을 나타낸다. 이를 시간 복잡도로 표현하자면, $O(2^{n})$이 된다.

다이나믹 프로그래밍

캐싱 방식 적용하기

기존의 재귀적 문제 풀이 방식에서의 가장 큰 문제는 같은 계산을 여러 번 하는 것이었다. 이러한 문제를 해결하기 위해 캐싱 방식을 사용하면 되지 않을까?

def fib(n):
    cache = {0: 0, 1: 1}
    def calc(n):
        if n in cache:
            return cache[n]
        else:
            cache[n] = calc(n-1) + calc(n-2)
            return cache[n]
    return calc(n)

fib(100)

캐싱을 하니 $n = 100$에 대한 값도 금방 나오는 것을 확인할 수 있다. 딕셔너리에 모든 값들을 캐싱하는 것이기 때문에, 나중에 값이 매우 커졌을 때 공간 복잡도에 문제가 발생하지 않을까 싶다.

시간복잡도를 보면 캐싱으로 인해 각 $n$에 대해 한 번만 계산을 수행하기 때문에 $O(n)$의 시간 복잡도를 얻을 수 있다.

그렇다면, 공간 복잡도를 줄이면서 $O(n)$의 시간 복잡도를 가질 순 없을까?

상향식으로 접근하기

위 방법 모두 $F_{n}$을 구하기 위해 $F_{n-1}$부터 $F_{0}$까지 $n$을 감소시켜가며 접근하였다.
반대로, $n$을 늘려가며 접근하는 방식은 어떨까?

def fib(n):
    if n == 0: return 0
    a, b = 0, 1
    for _ in range(2, n + 1):
        a, b = b, a + b
    return b

fib(100)

위 방식을 보면, a와 b를 각각 $0$, $1$로 두고, $2$부터 $n+1$까지 올라가며 계산을 진행한다.

하나의 반복문으로 계산을 진행하기 때문에 $O(n)$의 시간 복잡도를 갖는다.

행렬의 거듭제곱

백준 #11444. 피보나치 수 6를 풀면서 새롭게 알게 된 개념이다. 피보나치 수열은 행렬의 거듭제곱 형태로 표현이 가능하다.

어떻게 가능할까?

먼저, 피보나치 수열은 앞서 말했듯이, 다음과 같은 점화식을 나타낸다.

$F_{n+1} = F_{n} + F_{n-1}$

이를 행렬 형태로 나타내본다.

여기서 행렬곱의 결과가 좌변과 같아지려면, $A$는 다음과 같아야 한다.

여기서, 우변의 $\begin{pmatrix}F_n \\F_{n-1}\end{pmatrix}$ 또한 다음과 같이 나타낼 수 있다.

$(2)$번 수식과 $(3)$번 수식을 합치면 다음과 같이 거듭제곱으로 표현된다.

위 과정을 계속 진행하다 보면, 최종적으로 다음과 같은 수식이 나오게 된다.

$\begin{pmatrix}1 & 1 \\1 & 0\end{pmatrix}^{n}$ 행렬의 제곱을 풀어보면 다음과 같은 관계식을 갖는 것을 알 수 있다.

즉, 행렬의 첫 번째 행 첫 번째 열에 있는 값이 피보나치 수열의 $n$번째 값이 된다.

이를 코드로 구현하면 다음과 같다.

def multi(A: list, B: list) -> list:
    a11 = A[0][0]*B[0][0] + A[1][0]*B[0][1]
    a12 = A[0][0]*B[1][0] + A[1][0]*B[1][1]
    a21 = A[0][1]*B[0][0] + A[1][1]*B[0][1]
    a22 = A[0][1]*B[1][0] + A[1][1]*B[1][1]
    return [[a11, a12], [a21, a22]]

def power(F: list, n: int) -> list:
    result = F
    for _ in range(n - 2):
        result = multi(result, F)
    return result

def fib(n: int) -> int:
    F = [[1, 1], [1, 0]]
    return power(F, n)[0][0]

fib(100)

위 방식으르 활용하면 $O(n)$의 시간 복잡도를 얻을 수 있다.

여기서 지수의 특성을 활용해 분할 정복을 하게 되면 $O(\log{n})$까지 시간 복잡도를 줄여볼 수 있다.

def multi(A: list, B: list) -> list:
    a11 = A[0][0]*B[0][0] + A[1][0]*B[0][1]
    a12 = A[0][0]*B[1][0] + A[1][0]*B[1][1]
    a21 = A[0][1]*B[0][0] + A[1][1]*B[0][1]
    a22 = A[0][1]*B[1][0] + A[1][1]*B[1][1]
    return [[a11, a12], [a21, a22]]

def power(F: list, n: int):
	# 분할 정복을 활용한 거듭제곱
    if n == 0:
        return [[1, 0], [0, 1]]
    temp = power(F, n//2)
    result = multi(temp, temp)
    if n % 2 == 1:
        return multi(F, result)
    else:
        return result

def fib(n: int) -> int:
    F = [[1, 1], [1, 0]]
    return power(F, n-1)[0][0]

fib(100)

---

문제 풀어보기

#2747. 피보나치 수: 브론즈 문제임에도 불구하고 재귀를 이용한 단순 무식한 방법으로는 문제를 풀 수 없게 되어있다.

#11444. 피보나치 수 6: 일반적인 방식으로는 시간 초과가 뜨기 때문에, 모듈러 연산과 행렬의 거듭제곱 방식을 활용하여 문제를 해결해야 한다.