알고리즘: 이분 탐색(Binary Search)

이분 탐색이란?

정렬되어 있는 데이터 집합에서, 원하는 값을 빠르게 찾는 알고리즘.

전체를 순차적으로 탐색하는 대신, 항상 탐색 범위를 절반씩 줄여나가면서 원하는 값을 찾아나간다.

시간 복잡도는 $O(\log n)$으로 매우 빠른 탐색을 할 수 있다.

전제 조건

• 데이터가 정렬되어 있어야 한다.
• 데이터가 오름차순/내림차순 등으로 이미 정리되어 있지 않다면, 먼저 정렬해야 한다.

동작 과정

1. 탐색 범위의 중간값 mid를 찾는다.
2. 중간값이 찾는 값이면 종료한다.
3. 중간값보다 찾는 값이 작으면 왼쪽 구간만 탐색한다.
4. 중간값보다 찾는 값이 크면 오른쪽 구간만 탐색한다.
5. 탐색 구간이 없을 때까지 반복한다.

항상 절반씩 범위를 좁히기 때문에, $O(\log n)$이라는 빠른 속도를 가진다.

구현

이분 탐색으로 풀 수 있는 문제인 #1920. 수 찾기를 예시로 들어보자.

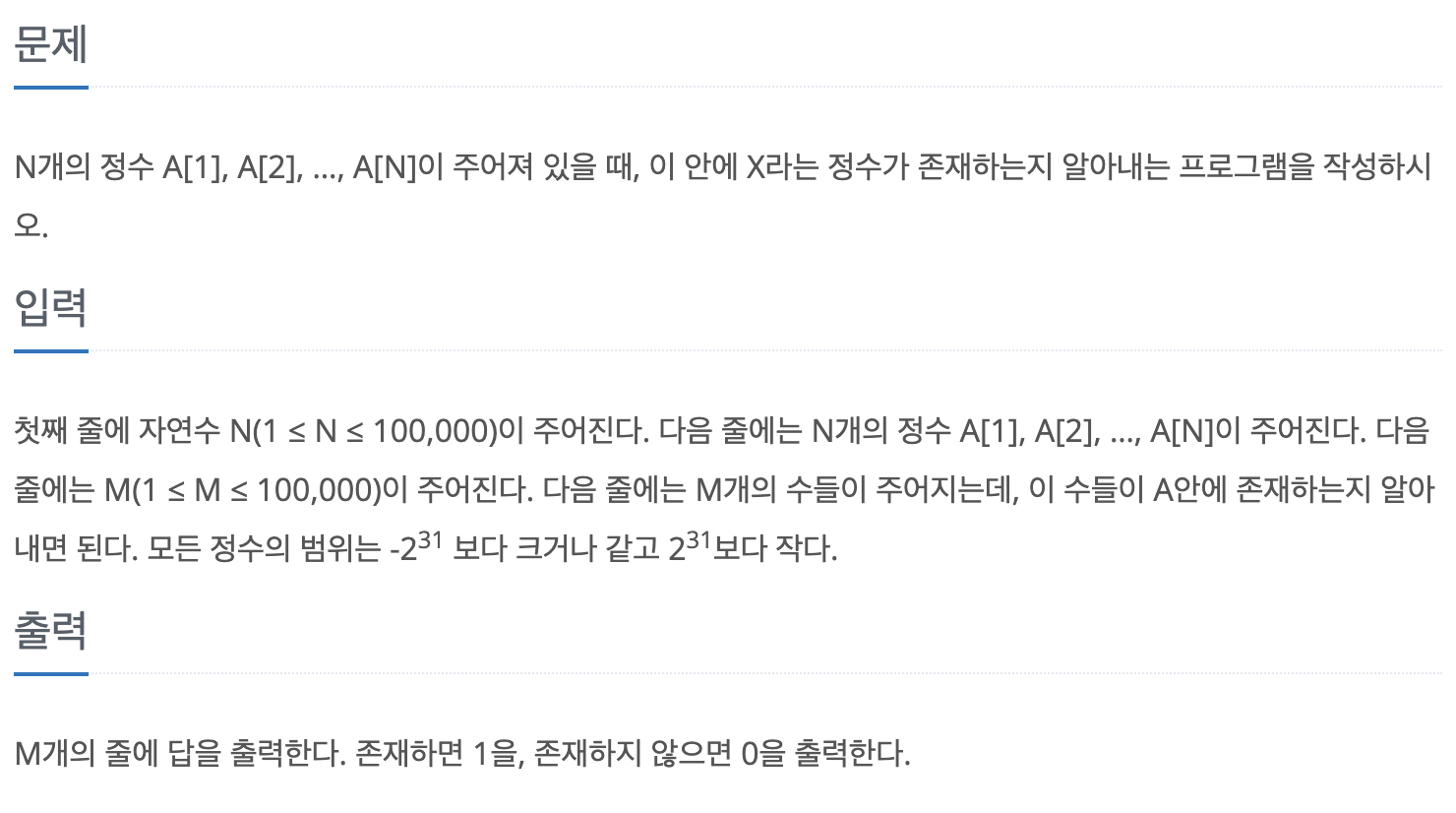
주어진 수열에서 특정 수가 존재하는지 아닌지만 판별하는 문제이다.

처음 떠올릴 수 있는 가장 직관적인 방법은, 단순히 모든 원소를 순회하면서 하나씩 비교하는 방식이다.

def find(target: int, seq: list) -> bool:
	for n in seq:
    	if n == target: return True
    return False

하지만 이 방법은 최악의 경우 모든 원소를 다 비교해야 하므로 $O(n)$이 걸린다.

특히 데이터가 수십만 개 이상일 경우, 시간 초과가 발생할 수 있다.

따라서 더 효율적인 방법인 이분 탐색을 사용해 문제를 해결할 수 있다.

def find(target: int, seq: list) -> bool:
    low = 0
    high = len(seq) - 1
    while low <= high:
        mid = (low + high) // 2
        if seq[mid] == target: return True
        elif seq[mid] < target: low = mid + 1
        else: high = mid - 1
    return False

여기서 seq는 반드시 정렬되어 있어야 한다. 정렬되어 있지 않으면, 이분 탐색은 올바르게 동작하지 않는다.

이처럼 탐색 문제에서 단순 반복문 대신 정렬 + 이분 탐색 패턴을 적용하면 시간복잡도를 대폭 줄여 효율적인 해결이 가능하다.